Principal Component Analysis (PCA)

Machine Learning → Unsupervised Learning → Dimensionality Reduction

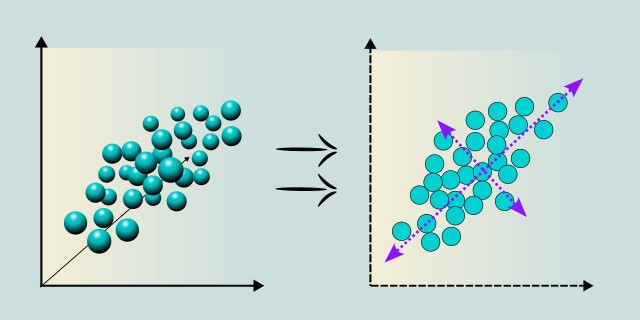
Principal Component Analysis is a dimensionality reduction method that belongs to the group of unsupervised learning techniques. Its goal is to transform the original data into a new coordinate system called principal components. These components capture as much variability in the data as possible. They are created as linear combinations of the original variables and are mutually uncorrelated (orthogonal). The first component captures the most variance, the second captures the most of the remaining variance, and so on. Simply put, the algorithm takes a large number of input variables and finds hidden patterns that capture the greatest differences in the data.

The result of applying PCA is a smaller, more compact dataset that retains as much of the original informational value as possible. This technique is useful as preprocessing before modeling or as a standalone tool for data exploration. It is especially useful when we have, for example, a large number of input variables that may be partially redundant or strongly correlated. Or if we want to simplify the model that will be trained on the data, or if we want to filter out noise and keep only the most important information. The method is also often used when we need to visualize data in 2D or 3D space.

How It Works

Principal Component Analysis works by finding new axes in the data space that best capture its structure. The goal is to transform the original coordinate system (formed by the individual variables) into a new one, where the data is spread out (has maximum variance) along as few directions (components) as possible. This process also ensures that the new axes are perpendicular (orthogonal) to each other and that there is no correlation between them.

Data Normalization

The first thing PCA does is normalize the data. This is an important step because PCA is highly sensitive to the scale of the variables. For example, if one feature (like weight) has a much larger numerical range than another feature (like height), it could dominate the analysis. To avoid this, the data is standardized by subtracting the mean of each variable and scaling it by its standard deviation. This ensures that each variable contributes equally to the analysis, regardless of its original scale.

Covariance Matrix Calculation

Once the data is normalized, the next step is to calculate the covariance matrix. This matrix describes how different variables in the dataset vary in relation to each other. If two variables are highly correlated, their covariance will be large. The covariance matrix is symmetric and captures the relationships between all pairs of variables, helping us understand how changes in one variable might correspond to changes in another.

Eigenvectors and Eigenvalues

Next, PCA finds the eigenvectors and eigenvalues of the covariance matrix. These are the key components that define the principal components:

Eigenvectors represent the directions in the data space where the variance is the highest. In simple terms, they define new axes along which the data can be projected.
Eigenvalues tell us how much variance each eigenvector (or principal component) captures. The larger the eigenvalue, the more important the corresponding eigenvector is in explaining the data's variance.

Sorting and Selecting Principal Components

Once the eigenvectors and eigenvalues are computed, PCA sorts the eigenvectors by the size of their eigenvalues. The eigenvector with the highest eigenvalue represents the direction of maximum variance in the data, and so on. To reduce the data’s dimensionality, PCA selects the top $k$ eigenvectors (those with the largest eigenvalues). These eigenvectors form a new set of axes, called the principal components, that capture the most significant patterns in the data.

Projecting the Data

Finally, the original data is projected onto the new coordinate system defined by the selected eigenvectors. This means that the data is transformed from its original high-dimensional space into a new, lower-dimensional space, where each new dimension corresponds to one of the principal components. The result is a dataset with fewer variables, but with most of the important information retained.

Mathematical Foundation

Suppose we have a dataset represented by an input matrix:

$$\mathbf{X} \in \mathbb{R}^{n \times p}$$

$\mathbf{X}$ is the data input matrix (dataset).
It has dimensions $n \times p$:
- $n$ is the number of observations (rows). For example, the number of measurements or records.
- $p$ is the number of variables (columns). For example, height, age, temperature, etc.

The goal of PCA is to find a transformation matrix:

$$\mathbf{W} \in \mathbb{R}^{p \times k}$$

$\mathbf{W}$ is the matrix computed by PCA containing $k$ principal components.
Its dimensions are $p \times k$:
- $n$ is the original number of variables.
- $p$ is the number of components we choose. For example, reducing 100 variables to 2 or 3 components.

The resulting transformed matrix will have the form:

$$\mathbf{Z} = \mathbf{X} \cdot \mathbf{W}$$

$\mathbf{Z} \in \mathbb{R}^{n \times k}$ is the matrix containing the reduced data.
Each row of $\mathbf{Z}$ is the projection of one observation into the space of $k$ principal components.
The result is a dataset with the same number of rows (observations) but fewer columns (components).

Thus, we project the data from the original high-dimensional space into a lower-dimensional space.

Procedure

1. Data Normalization

Before applying PCA, each variable must be normalized, typically by standardizing to zero mean and unit standard deviation. PCA is sensitive to the scale of values, and variables may have different ranges (e.g., height in cm vs. weight in kg), which could distort the results.

Normalization is performed by the formula:

$$x_{ij}' = \frac{x_{ij} - \bar{x}_j}{\sigma_j}$$

$x_{ij}$ is the value for the $i$-th row (observation) and $j$-th column (variable).
$\bar{x}_j$ is the mean of variable $j$.
$\sigma_j$ is the standard deviation of variable $j$.
$x_{ij}'$ is the resulting standardized value.

2. Computing the Covariance Matrix

From the standardized data, compute the covariance matrix $\mathbf{C}$, which captures the mutual dependencies between variables:

$$\mathbf{C} = \frac{1}{n-1} \mathbf{X}^T \mathbf{X}$$

$\mathbf{X}$ is the matrix of standardized data.
$\mathbf{X}^T$ is the transpose of $\mathbf{X}$.
$\mathbf{C}$ is a symmetric covariance matrix.

3. Calculating Eigenvectors and Eigenvalues

Compute eigenvectors $\mathbf{v}$ and eigenvalues $\lambda$ from the covariance matrix, corresponding to the directions of maximum variance in the data:

$$\mathbf{C} \cdot \mathbf{v} = \lambda \cdot \mathbf{v}$$

$\mathbf{v}$ is an eigenvector (direction of a principal component).
$\lambda$ is the eigenvalue (amount of variance captured by this component).

4. Selecting Principal Components

Sort the eigenvectors by their eigenvalues from largest to smallest and select the first $k$ components that capture a sufficient amount of variance (e.g., 95%).

5. Projecting Data into the New Space

Finally, project the original data onto the new coordinate system:

$$\mathbf{Z} = \mathbf{X} \cdot \mathbf{W}$$

$\mathbf{X}$ is the standardized data.
$\mathbf{W}$ is the matrix of selected eigenvectors.
$\mathbf{Z}$ is the data in the reduced space.

Result

By applying PCA, we obtain a more compact dataset with fewer dimensions while preserving most of the original informational value. For example, if the first principal component explains 70% of the variance and the second 20%, these two components together capture 90% of the information from the original data but in a much lower-dimensional space.

Sample Example

Let’s consider a simple case with only 2 observations of 2 variables.

Input Dataset / Input Matrix

$$\mathbf{X} = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$$

Rows: individual observations (e.g., two people).
Columns: two variables (e.g., height, weight).

Data Standardization

We calculate the mean of each variable (column):

Column 1: $\frac{2 + 0}{2} = 1$
Column 2: $\frac{0 + 2}{2} = 1$

$$\mathbf{X}_{\text{centered}} = \begin{bmatrix} 2 - 1 & 0 - 1 \\ 0 - 1 & 2 - 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$$

Covariance Matrix Calculation

$$\mathbf{C} = \frac{1}{n - 1} \cdot \mathbf{X}^T \cdot \mathbf{X}$$

There are 2 observations, so $n = 2$, which gives:

$$\mathbf{C} = \frac{1}{1} \cdot \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}^T \cdot \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$$

Multiplying the matrices:

$$\mathbf{C} = \begin{bmatrix} 1\cdot1 + (-1)\cdot(-1) & 1\cdot(-1) + (-1)\cdot1 \\ -1\cdot1 + 1\cdot(-1) & -1\cdot(-1) + 1\cdot1 \end{bmatrix} = \begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix}$$

Eigenvalues and Eigenvectors

To find the eigenvalues $\lambda$, solve the characteristic equation:

$$\det(\mathbf{C} - \lambda \mathbf{I}) = 0$$

$$\begin{vmatrix} 2 - \lambda & -2 \\ -2 & 2 - \lambda \end{vmatrix} = 0 \Rightarrow (2 - \lambda)^2 - (-2)^2 = 0 \Rightarrow (2 - \lambda)^2 = 4 \Rightarrow 2 - \lambda = \pm 2$$

The eigenvalues are: $\lambda_1 = 4$ and $\lambda_2 = 0$.

Eigenvectors

Let’s find eigenvectors for each $\lambda$:

For $\lambda_1 = 4$:

Solve $(\mathbf{C} - 4\mathbf{I})\mathbf{v} = 0$:

$$ \begin{bmatrix} -2 & -2 \\ -2 & -2 \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0 \Rightarrow -2v_1 - 2v_2 = 0 \Rightarrow v_1 = -v_2 $$

So the eigenvector (unit direction chosen arbitrarily):

$$\mathbf{v}_1 = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$$

For $\lambda_2 = 0$:

Solve $(\mathbf{C} - 0\mathbf{I})\mathbf{v} = \mathbf{C} \cdot \mathbf{v} = 0$:

$$\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \cdot \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0 \Rightarrow 2v_1 - 2v_2 = 0 \Rightarrow v_1 = v_2$$

So:

$$\mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$$

Selecting Components and Projecting the Data

We choose only 1 component (the one with the highest eigenvalue, $\lambda = 4$):

$$\mathbf{w} = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$$

Now project the centered data onto this new direction:

$$\mathbf{Z} = \mathbf{X}_{\text{centered}} \cdot \mathbf{w} = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ -1 \end{bmatrix} = \begin{bmatrix} 1\cdot1 + (-1)\cdot(-1) \\ -1\cdot1 + 1\cdot(-1) \end{bmatrix} = \begin{bmatrix} 2 \\ -2 \end{bmatrix}$$

Result

The original 2D data was:

$$\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$$

After applying PCA (with dimensionality reduced to 1), we obtained:

$$\\mathbf{Z} = \begin{bmatrix} 2 \\ -2 \end{bmatrix}$$

Code Example

Dependencies

Add to your Cargo.toml:

[dependencies]
nalgebra = "0.32"

Code

/// This example demonstrates how to perform Principal Component Analysis (PCA)
/// on a 3D dataset.

fn main() {
    // 1. Original data (4 observations, 3 variables)
    let x = vec![
        vec![2.0, 0.0, 1.0],
        vec![0.0, 2.0, 3.0],
        vec![1.0, 1.0, 0.0],
        vec![3.0, 1.0, 2.0],
    ];

    // 2. Calculate means (average for each column)
    let mean: Vec<f64> = (0..x[0].len())
        .map(|j| x.iter().map(|row| row[j]).sum::<f64>() / x.len() as f64)
        .collect();

    // 3. Centering the data
    let x_centered: Vec<Vec<f64>> = x
        .iter()
        .map(|row| row.iter().zip(mean.iter()).map(|(v, m)| v - m).collect())
        .collect();

    // 4. Calculate covariance matrix
    let xt = transpose(&x_centered);
    let c = matmul(&xt, &x_centered);

    // 5. Print covariance matrix
    println!("Covariance matrix:");
    print_matrix(&c);

    // 6. Manually enter eigenvectors (known from analysis or calculation)
    // Example eigenvectors, in practice these would be calculated from the covariance matrix
    let eigenvectors = vec![
        vec![1.0, 0.0, 0.0], // principal component 1
        vec![0.0, 1.0, 0.0], // principal component 2
        vec![0.0, 0.0, 1.0], // principal component 3
    ];

    // 7. Select the top principal components (eigenvectors with largest eigenvalues)
    let w = eigenvectors[0].clone(); // [1, 0, 0] (this could be the first principal component)

    // 8. Project data into 1D space (using the first principal component)
    let z: Vec<f64> = x_centered
        .iter()
        .map(|row| dot_product(row, &w))
        .collect();

    println!("Projected data onto first principal component:");
    for val in z {
        println!("{:.2}", val);
    }
}

// Helper functions:

// Transpose a matrix represented as a vector of vectors
// Each inner vector represents a row of the matrix
fn transpose(matrix: &[Vec<f64>]) -> Vec<Vec<f64>> {
    let rows = matrix.len();
    let cols = matrix[0].len();
    (0..cols)
        .map(|j| (0..rows).map(|i| matrix[i][j]).collect())
        .collect()
}

// Matrix multiplication
fn matmul(a: &[Vec<f64>], b: &[Vec<f64>]) -> Vec<Vec<f64>> {
    let rows = a.len();
    let cols = b[0].len();
    let mut result = vec![vec![0.0; cols]; rows];
    for i in 0..rows {
        for j in 0..cols {
            result[i][j] = (0..a[0].len()).map(|k| a[i][k] * b[k][j]).sum();
        }
    }
    result
}

// Computes the dot product of two vectors
// a and b must have the same length
fn dot_product(a: &[f64], b: &[f64]) -> f64 {
    a.iter().zip(b.iter()).map(|(x, y)| x * y).sum()
}

fn print_matrix(m: &[Vec<f64>]) {
    for row in m {
        println!("{:?}", row);
    }
}

Model Evaluation

Since PCA is an unsupervised learning technique, traditional classification metrics (like accuracy or precision) are not applicable. Instead, PCA evaluation focuses on variance preservation, reconstruction accuracy, and visual interpretability.

Explained Variance

The most common metric for evaluating PCA is the explained variance. Each principal component captures a portion of the total variance in the data. By summing the variances of the selected components, we obtain a measure of how much of the original information has been retained.

$$\text{Explained Variance Ratio}_k = \frac{\sum_{i=1}^{k} \lambda_i}{\sum_{j=1}^{p} \lambda_j}$$

$\lambda\_i$ is the eigenvalue (variance) of the $i$-th component.
$k$ is the number of selected components.
$p$ is the total number of original features.

A higher explained variance ratio indicates that the selected components retain more information from the original dataset. In practice, retaining 95% to 99% of the variance is often considered sufficient.

Reconstruction Error

If dimensionality reduction is followed by data reconstruction (inverse transformation), we can compute the reconstruction error to assess how well the reduced representation approximates the original data:

$$\text{Reconstruction Error} = \| \mathbf{X} - \hat{\mathbf{X}} \|_F$$

$\mathbf{X}$ is the original data matrix.
$\hat{\mathbf{X}}$ is the reconstructed matrix using selected components.
$| \cdot |\_F$ is the Frobenius norm, which measures the reconstruction error.

Lower reconstruction error indicates that important patterns and relationships in the data were preserved during the dimensionality reduction.

Scree Plot

A scree plot is a graphical tool used to visualize the eigenvalues (variances) associated with each principal component. The plot typically shows a steep drop followed by a plateau. The “elbow” point, where the slope levels off, suggests a good trade-off between dimensionality and variance retention.

Visualization (2D/3D)

PCA is often used for data visualization. Projecting high-dimensional data into 2D or 3D space allows us to visually inspect patterns, clusters, or outliers. If the reduced data shows clear structure or separability, it suggests that the principal components captured meaningful variation in the data.

Downstream Task Performance

Although PCA is unsupervised, its utility can also be indirectly evaluated through downstream tasks (e.g., classification or clustering). If the model trained on PCA-reduced features performs comparably to the model trained on the original data, it indicates that the essential information was retained.

Alternative Algorithms

When performing dimensionality reduction, Principal Component Analysis (PCA) is a widely used technique due to its simplicity and effectiveness. However, it may not always be the best choice; especially for nonlinear or class-dependent structures in the data.

t-distributed Stochastic Neighbor Embedding: t-SNE is a nonlinear dimensionality reduction technique particularly well-suited for visualizing high-dimensional data in 2D or 3D. It focuses on preserving local structures by converting similarities between points into probabilities and minimizing the divergence between high-dimensional and low-dimensional distributions. Learn more
Uniform Manifold Approximation and Projection: UMAP is a nonlinear dimensionality reduction technique based on manifold theory and fuzzy topological structures. It is similar to t-SNE in visualization but faster and more scalable, while also preserving more of the global structure.
Linear Discriminant Analysis: LDA is a supervised dimensionality reduction method that seeks to project data onto a lower-dimensional space that maximizes class separability. Unlike PCA, which is unsupervised, LDA considers class labels.
Autoencoders: Autoencoders are a type of neural network used for unsupervised representation learning. They compress data into a latent space and then reconstruct the original input. The encoder part can be used for dimensionality reduction.

Advantages and Disadvantages

Principal Component Analysis (PCA) is a powerful technique for dimensionality reduction, widely used in preprocessing and exploratory data analysis. While it helps simplify datasets and uncover hidden patterns, it also comes with certain trade-offs—especially in terms of interpretability and sensitivity to data quality.

✅ Advantages:

Reduces dimensionality and lowers computational requirements.
Eliminates redundancy and collinearity (removal of dependent features).
Simplifies data visualization (e.g., 2D projection from 10D space).
Can improve the performance of other algorithms (e.g., classification models).

❌ Disadvantages:

Principal components are not easily interpretable (they are combinations of features).
Based solely on variance, it may not capture structures relevant to classification tasks.
Sensitive to scaling and outliers.
Does not preserve the original meaning of attributes.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🟢 Low

Use Case Examples

Data Visualization

PCA is frequently used to reduce high-dimensional data to 2 or 3 dimensions for plotting and visual analysis. This helps in identifying clusters, patterns, or outliers that may not be obvious in higher-dimensional space.

Noise Reduction in Signals

In sensor data or image processing, PCA can help filter out noise by keeping only the most significant components. This improves signal quality while discarding less relevant variations caused by measurement error or environmental interference.

Gene Expression Analysis (Bioinformatics)

PCA is applied to analyze gene expression data from microarray or RNA-seq experiments. It reduces thousands of gene variables to a few principal components, allowing researchers to identify dominant patterns or clusters among patient samples.

Anomaly Detection

By projecting data into a lower-dimensional space, PCA helps in identifying deviations from the norm. Points that lie far from the principal components can be flagged as anomalies, useful in fraud detection or industrial monitoring.

Feature Reduction for Machine Learning

Before training models, PCA can be used to reduce the number of features while preserving most of the information. This helps improve training speed, reduce overfitting, and enhance model generalization; especially in high-dimensional datasets.

Conclusion

Principal Component Analysis (PCA) is a foundational tool in data science and machine learning, especially useful when dealing with high-dimensional datasets. By transforming the original features into a smaller set of uncorrelated components, PCA helps reduce complexity, remove noise, and reveal latent patterns in the data.

Although it does not preserve the original features and may be less effective in tasks where interpretability is critical, its ability to compress information while retaining most of the variance makes it a valuable step in many data preprocessing pipelines. When applied thoughtfully, PCA can enhance both model performance and understanding of the underlying data structure.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.