Logistic Regression

Machine Learning → Supervised Learning → Classification → Single Label Classification → Binary Classification

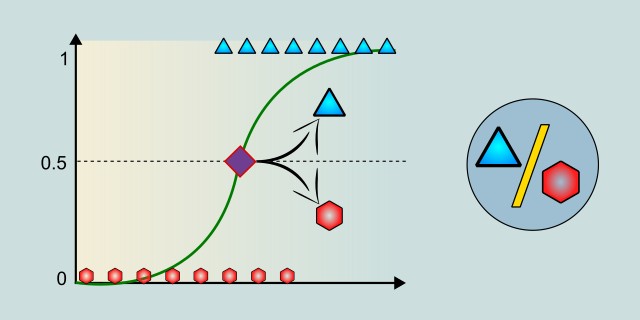
Logistic Regression is a statistical method used to model the probability of a certain class or event occurring. Despite the name "regression", it is actually a classification algorithm, most commonly used for binary classification, such as making decisions between two possible outcomes (e.g. yes/no, sick/healthy, spam/not spam). Logistic regression predicts the probability that a given input belongs to a particular class (e.g. the probability that a customer will buy a product). The output is not only a class assignment but also a calculated probability associated with the prediction.

How It Works

Logistic regression is a model that attempts to find a relationship between the input data (called "features") and a target variable that has only two possible values (0 or 1, "yes" or "no", "true" or "false", etc.). The goal of the model is to estimate the probability that a given input belongs to a certain class, most often class 1 (the positive class). This estimate can then be used for a classification decision: if the probability is greater than a certain threshold (for example 0.5), we predict class 1; otherwise, class 0.

Logistic regression first computes a linear combination of the input features, similar to classical linear regression. Each input has its own weight that determines its influence on the outcome.

The result of the linear combination is an arbitrary real number, which is not suitable as a probability prediction. Therefore, this output is transformed using the sigmoid function, which ensures that the result is in the range between 0 and 1.

The final value represents the probability that the input belongs to class 1. Based on the selected threshold, we then decide which class to predict.

Mathematical Foundation

Logistic regression uses a combination of linear algebra and a probabilistic transformation to estimate the probability that a given input belongs to class 1 (for example, a "positive" case).

Linear Combination

The first step is to compute a linear combination of the input variables:

$$z = w_0 + w_1x_1 + w_2x_2 + \dots + w_nx_n = \mathbf{w}^\top \mathbf{x}$$

or in vector form:

$$z = \mathbf{w}^\top \mathbf{x}$$

$\mathbf{x} = (x_1, x_2, \dots, x_n)$ – is the vector of input features.
$\mathbf{w} = (w_1, w_2, \dots, w_n)$ – are the weights (model parameters).
$w_0$ – is the bias (intercept).
$z$ – is the output of this linear part. It can be negative, positive, or zero, and it is not a probability.

Sigmoid (Logistic) Function

Transforms $z$ into a probability:

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$

This function maps any real number to the interval $[0, 1]$, which is ideal for probabilities.

👉 For more details on the sigmoid function, see the Sigmoid Function page.

Probability Prediction

$$P(y = 1 | \mathbf{x}) = \sigma(\mathbf{w}^\top \mathbf{x})$$

For very large $z$, $\sigma(z) \to 1$
For very small $z$, $\sigma(z) \to 0$
For $z = 0$, $\sigma(z) = 0.5$

The result is a number between 0 and 1, interpreted as the probability that the output class is 1.

$$P(y = 1 \mid \mathbf{x}) = \hat{y} = \sigma(z)$$

Loss Function (Log Loss / Cross-Entropy)

To train the model to make good predictions, we must compare its output $\hat{y}$ with the true result $y \in {0, 1}$. The commonly used loss function is the logarithmic loss (log loss):

$$\mathcal{L}(y, \hat{y}) = - \left( y \cdot \log(\hat{y}) + (1 - y) \cdot \log(1 - \hat{y}) \right)$$

This function has several important properties:

It penalizes heavily when the model is "confident" (e.g., $\hat{y} = 0.99$) but wrong.
It works well with probabilistic outputs.
It is convex, allowing efficient optimization.

Model Training – Gradient Descent

To minimize the loss, an optimization method called gradient descent is used. The goal is to find weights $\mathbf{w}$ that minimize the total loss on the training data.

Weights are updated according to the formula:

$$\mathbf{w} := \mathbf{w} - \alpha \cdot \nabla_{\mathbf{w}} \mathcal{L}$$

$\alpha$ – is the learning rate, which determines the size of the steps we take.
$\nabla_{\mathbf{w}} \mathcal{L}$ – is the gradient, the direction to move in order to reduce the loss.

This process is repeated (iteratively) until the weights stabilize and the loss stops decreasing.

Code Example

Basic implementation of linear regression in Rust using gradient descent. It models the relationship between a single input and output variable by iteratively updating the weight and bias to minimize prediction error. The loss function used is Mean Squared Error (MSE), which is commonly applied in regression problems. While it handles only one feature, the same principles can be extended to support multiple inputs in a multiple linear regression model.

/// Sigmoid function for logistic regression
fn sigmoid(z: f64) -> f64 {
    1.0 / (1.0 + (-z).exp())
}

/// Trains logistic regression using gradient descent
fn train_logistic_regression(
    x_data: &[f64],
    y_data: &[f64],
    learning_rate: f64,
    epochs: usize,
    print_loss: bool,
) -> (f64, f64) {
    let mut w = 0.0;
    let mut b = 0.0;
    let n = x_data.len() as f64;
    for epoch in 0..epochs {
        let mut dw = 0.0;
        let mut db = 0.0;
        for i in 0..x_data.len() {
            let x = x_data[i];
            let y = y_data[i];
            let z = w * x + b;
            let y_pred = sigmoid(z);
            dw += (y_pred - y) * x;
            db += y_pred - y;
        }
        dw /= n;
        db /= n;
        w -= learning_rate * dw;
        b -= learning_rate * db;
        if print_loss && epoch % 200 == 0 {
            let loss: f64 = x_data.iter()
                .zip(y_data.iter())
                .map(|(&x, &y)| {
                    let y_pred = sigmoid(w * x + b);
                    -y * y_pred.ln() - (1.0 - y) * (1.0 - y_pred).ln()
                })
                .sum::<f64>() / n;
            println!("Epoch {}: Loss = {:.4}, w = {:.4}, b = {:.4}", epoch, loss, w, b);
        }
    }
    (w, b)
}

/// Predicts the probability for a given input using trained parameters
fn predict_proba(x: f64, w: f64, b: f64) -> f64 {
    sigmoid(w * x + b)
}

/// Predicts the class (0 or 1) for a given input using trained parameters
fn predict_class(x: f64, w: f64, b: f64) -> u8 {
    if predict_proba(x, w, b) > 0.5 { 1 } else { 0 }
}

fn main() {
    // Training data: inputs (x) and binary target outputs (y)
    let x_data = vec![1.0, 2.0, 3.0, 4.0, 5.0];
    let y_data = vec![0.0, 0.0, 0.0, 1.0, 1.0];

    // Training hyperparameters
    let learning_rate = 0.1;
    let epochs = 2000;

    // Train the model
    let (w, b) = train_logistic_regression(&x_data, &y_data, learning_rate, epochs, true);

    // Final model parameters
    println!("\nTrained logistic regression: y = sigmoid({:.4} * x + {:.4})", w, b);

    // Prediction for a new input
    let test_x = 5.0;
    let prob = predict_proba(test_x, w, b);
    let predicted_class = predict_class(test_x, w, b);
    println!("Prediction for x = {} → probability = {:.4}, class = {}", test_x, prob, predicted_class);
}

Model Evaluation

To determine whether our classification model (e.g., logistic regression) makes accurate predictions, we need to compare its outputs with the actual values in the test dataset. Various performance metrics are used for this purpose, each evaluating a different aspect of the model's behavior.

Confusion Matrix

The confusion matrix compares true classes with predicted classes. It looks like this:

	Predicted Positive	Predicted Negative
Actual Positive	TP	FN
Actual Negative	FP	TN

TP (True Positives) – Correctly predicted positive cases.
TN (True Negatives) – Correctly predicted negative cases.
FP (False Positives) – Incorrectly predicted positive cases.
FN (False Negatives) – Incorrectly predicted negative cases.

Accuracy

Indicates the percentage of total predictions that were correct:

$$\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}$$

If the dataset is imbalanced (e.g., 95% of class 0), accuracy can be misleading.

👉 A detailed explanation of Accuracy can be found in the section: Accuracy

Precision

Out of the cases where the model predicted class 1, how many were actually correct?

$$\text{Precision} = \frac{TP}{TP + FP}$$

Important when false positives are problematic (e.g., labeling a valid email as spam).

👉 A detailed explanation of Precision can be found in the section: Precision

Recall (Sensitivity)

Out of the actual class 1 cases, how many did the model correctly identify?

$$\text{Recall} = \frac{TP}{TP + FN}$$

Crucial when we want to avoid missing any positive cases (e.g., disease detection).

👉 A detailed explanation of Recall can be found in the section: Recall

F1 Score

F1 score is the harmonic mean of precision and recall. It is used when a balance between both metrics is desired.

$$\text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$$

Especially useful for imbalanced class distributions.

👉 A detailed explanation of F1 Score can be found in the section: F1 Score

ROC Curve and AUC

The ROC curve (Receiver Operating Characteristic) plots the relationship between True Positive Rate and False Positive Rate across different classification thresholds.

$$\text{TPR} = \frac{TP}{TP + FN}$$

AUC (Area Under the Curve) represents the area under the ROC curve and indicates how well the model separates the classes.

$$\text{FPR} = \frac{FP}{FP + TN}$$

AUC = 0.5 indicates random guessing, while AUC = 1.0 indicates perfect classification.

Alternative Algorithms

For more complex data, there are several more sophisticated classification algorithms that may yield better results.

Decision Trees Unlike logistic regression, decision trees can model non-linear relationships and don’t require data normalization. However, they can be unstable and prone to overfitting, especially on complex datasets.Learn more
Random Forest: Random Forest often outperforms logistic regression in accuracy by combining multiple decision trees and reducing overfitting. On the downside, it is less interpretable and more computationally intensive, which can be a limitation in large-scale or real-time applications. Learn more
Support Vector Machines (SVM): SVM performs better than logistic regression on high-dimensional data and non-linearly separable problems. It does require careful tuning of hyperparameters and can be slow with large datasets. Learn more
K-Nearest Neighbors (K-NN): K-NN is a simple, training-free model that can capture non-linear class boundaries, something logistic regression struggles with. However, it is much slower during prediction and sensitive to parameter choices and feature scaling. Learn more
Neural Networks: Neural networks greatly outperform logistic regression on complex tasks by learning intricate, non-linear patterns in data. Their main drawbacks are poor interpretability, the need for large amounts of data, and high computational demands. Learn more

Advantages and Disadvantages

✅ Advantages:

Simple and easy to interpret.
Fast and efficient, even with large datasets.
Serves as a good baseline method for classification tasks.
Outputs probabilities, not just hard decisions.

❌ Disadvantages:

Assumes a linear relationship between the inputs and the log-odds of the probability.
Performs poorly when data relationships are highly complex (in such cases, models like decision trees, SVMs, or neural networks may be more suitable).
Sensitive to multicollinearity between input variables.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🟢 Low

Use Case Examples

Email Spam Detection

Classifying whether an email is spam or not based on its content. Logistic regression helps identify patterns in words or metadata that indicate spam messages.

Customer Churn Prediction

Predicting whether a customer will stop using a service. This helps businesses proactively engage with at-risk customers by modeling behavioral indicators of churn.

Medical Diagnosis

Determining whether a patient has a certain disease based on test results and symptoms. Logistic regression provides a probability that can assist doctors in making diagnostic decisions.

Loan Approval

Assessing whether a loan applicant is likely to repay the loan. Logistic regression uses features like income, credit score, and employment history to estimate risk.

Marketing Response Prediction

Predicting if a customer will respond to a marketing campaign. By analyzing past campaign data, logistic regression can help target the right audience more effectively.

Conclusion

Logistic regression is a fundamental algorithm for binary classification with a clear mathematical foundation and provides interpretable results. It is often the first choice in practice because it is fast, stable, and can be extended to multi-class classification using softmax regression.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.