Decision Tree Regression

Machine Learning → Supervised Learning → Regression → Non-Linear Regression

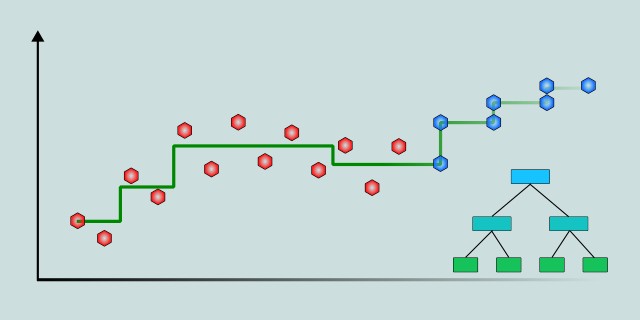
Decision trees are versatile machine learning algorithms that can be used not only for classification but also for regression problems. In regression, decision trees predict continuous numerical values rather than discrete classes. This flexibility allows them to model complex relationships between input features and target variables without assuming any specific functional form. Decision tree regression is widely used in various fields such as finance, engineering, and environmental science because of its interpretability, ease of use, and ability to capture non-linear patterns in data.

How It Works

Decision tree regression works by recursively splitting the dataset into smaller groups based on feature values, aiming to create subsets that are as homogeneous as possible with respect to the target variable. At each step, the algorithm selects the feature and split point that minimize the variance (or another impurity measure) within the resulting groups.

The tree continues to grow until it reaches a stopping condition, such as when all data points in a node have similar target values, a maximum depth is reached, or further splits no longer significantly reduce the variance.

Once the tree is built, predictions for new data points are made by following the path from the root node down to a leaf node, where the average target value of the training samples in that leaf is returned as the prediction. Thanks to this structure, decision tree regression models are interpretable. We can closely monitor how the prediction is made by tracking the distributions leading to the leaf node.

Imagine you want to predict the price of a house based on its features like size, number of bedrooms, and location. A decision tree regression model will start by looking at the entire dataset and deciding which feature and value best splits the houses into groups that have similar prices. For example, it might first split houses by whether they are larger or smaller than 150 square meters.

Then, within each group, the tree will keep splitting the data further. For instance, it might separate houses by the number of bedrooms or by neighborhood, always aiming to group houses with more similar prices together.

This process continues until the groups are small enough or until further splitting does not improve the prediction much. To predict the price of a new house, the model follows the same sequence of splits based on the house’s features and ends up in a group (leaf) where it assigns the average price of all houses in that group as the predicted value.

Mathematical Foundation

The goal of decision tree regression is to split the data into regions where the target variable (the value we want to predict) is as consistent as possible. In other words, the algorithm tries to group similar values together by repeatedly dividing the dataset based on the input features.

How Splitting Works

At each step in the tree (called a node), the algorithm considers every feature and potential split point. It selects the one that best divides the data into two groups:

$$R_1(j, s) = \{ \mathbf{x} \mid x_j \leq s \}, \quad R_2(j, s) = \{ \mathbf{x} \mid x_j > s \}$$

$j$ is the index of the feature (like size, number of rooms).
$s$ is the value used as a split point.
$R_1$ and $R_2$ are the two resulting regions after the split.

The algorithm chooses the split that minimizes the sum of squared errors within the two new regions:

$$\min_{j, s} \left[ \sum_{x_i \in R_1(j,s)} (y_i - \bar{y}_{R_1})^2 + \sum_{x_i \in R_2(j,s)} (y_i - \bar{y}_{R_2})^2 \right]$$

$y_i$ is the actual target value (e.g., price of a house).
$\bar{y}_{R_k}$ is the average of the target values in region $R_k$.

$$\bar{y}_{R_k} = \frac{1}{|R_k|} \sum_{x_i \in R_k} y_i$$

This average is what the model will use for predictions in that region.

More Intuitive

Let's imagine that you are trying to predict real estate prices. If you group properties according to whether they are larger or smaller than 150 square meters, you will find that prices are more consistent within each group. The algorithm tries to find the best such division based on all available characteristics.

Let’s say you split the houses into:

Group A: [200,000; 210,000; 205,000] → Average = 205,000
Group B: [500,000; 510,000; 495,000] → Average = 501,667

This is a good split because both groups have values close to their group average, which means the error is small. The decision tree will keep making such splits until each group (or leaf) is small and consistent enough, or until further splitting no longer improves the result.

Prediction

For a new input $\mathbf{x}$, the tree identifies the region $R_m$ it belongs to, and the predicted value $\hat{y}$ is simply the average of the target values in that region:

$$\hat{y} = \bar{y}_{R_m}$$

Once the tree is built, predicting a new value is simple.

Take the new input.
Follow the tree's decisions based on its features.
Reach a leaf node that contains a group of training samples.

Code Example

In this example, we will implement a basic regression decision tree. We will create a small dataset, then create a simple decision tree that divides the data based on a single feature, and finally use it to predict the value for a new data point.

// Define a data point with features and a target value
#[derive(Debug, Clone)]
struct DataPoint {
    feature: f64,
    target: f64,
}

// Define a simple decision tree node
#[derive(Debug)]
enum TreeNode {
    Leaf(f64), // Prediction is a constant value (mean of the region)
    Node {
        threshold: f64,
        left: Box<TreeNode>,
        right: Box<TreeNode>,
    },
}

// Function to compute the mean target value of a region
fn mean_target(data: &[DataPoint]) -> f64 {
    let sum: f64 = data.iter().map(|d| d.target).sum();
    sum / data.len() as f64
}

// Function to compute the variance (sum of squared errors)
fn variance(data: &[DataPoint]) -> f64 {
    let mean = mean_target(data);
    data.iter().map(|d| (d.target - mean).powi(2)).sum()
}

// Train a simple regression tree (1-level split)
fn build_tree(data: &[DataPoint]) -> TreeNode {
    let mut best_threshold = 0.0;
    let mut best_score = f64::INFINITY;
    let mut best_left = vec![];
    let mut best_right = vec![];

    // Try each unique feature value as a possible split point
    for point in data {
        let threshold = point.feature;
        let left: Vec<_> = data.iter().cloned().filter(|d| d.feature <= threshold).collect();
        let right: Vec<_> = data.iter().cloned().filter(|d| d.feature > threshold).collect();

        if left.is_empty() || right.is_empty() {
            continue;
        }

        let score = variance(&left) + variance(&right);
        if score < best_score {
            best_score = score;
            best_threshold = threshold;
            best_left = left;
            best_right = right;
        }
    }

    // If no useful split is found, return a leaf
    if best_score == f64::INFINITY {
        return TreeNode::Leaf(mean_target(data));
    }

    TreeNode::Node {
        threshold: best_threshold,
        left: Box::new(build_tree(&best_left)),
        right: Box::new(build_tree(&best_right)),
    }
}

// Predict target value using the trained tree
fn predict(tree: &TreeNode, feature: f64) -> f64 {
    match tree {
        TreeNode::Leaf(value) => *value,
        TreeNode::Node { threshold, left, right } => {
            if feature <= *threshold {
                predict(left, feature)
            } else {
                predict(right, feature)
            }
        }
    }
}

fn main() {
    // Sample dataset
    let data = vec![
        DataPoint { feature: 1.0, target: 2.0 },
        DataPoint { feature: 2.0, target: 4.0 },
        DataPoint { feature: 3.0, target: 6.0 },
        DataPoint { feature: 4.0, target: 8.0 },
    ];

    // Train the tree
    let tree = build_tree(&data);

    // Predict on a new sample
    let new_feature = 2.5;
    let prediction = predict(&tree, new_feature);
    println!("Prediction for input {:.1}: {:.2}", new_feature, prediction);
}

This example shows how a very simple decision tree can be implemented from scratch in Rust. While real-world use typically relies on optimized libraries (e.g. linfa), this code serves as a basic illustration of the underlying principles.

Model Evaluation

When evaluating a decision tree regression model, we use metrics that measure how close the predicted values are to the actual continuous target values. These metrics help determine whether the model is making accurate and reliable predictions.

MAE (Mean Absolute Error)

Mean Absolute Error (MAE) is a metric used to evaluate regression models by measuring the average absolute difference between actual and predicted values. MAE treats all errors equally, making it more robust to outliers and noise in the data.

It represents the average absolute difference between the actual and predicted values:

$$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$

👉 A detailed explanation of MAE can be found in the section: Mean Absolute Error

MSE (Mean Squared Error)

MSE penalizes larger errors more than smaller ones (because the error is squared).

It represents the average squared difference between the actual and predicted values:

$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$

👉 A detailed explanation of MSE can be found in the section: Mean Squared Error

RMSE (Root Mean Squared Error)

RMSE has the same units as the original values, making it more intuitive to interpret.

It represents the average squared difference between the actual and predicted values:

$$ \text{RMSE} = \sqrt{\text{MSE}} $$

👉 A detailed explanation of RMSE can be found in the section: Root Mean Squared Error

R² (Coefficient of Determination)

R² indicates how much of the variability in the data can be explained by the model:

$$ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} $$

Close to 1 – the model explains the variability in the data very well.
Close to 0 – the model explains very little of the variability.

👉 A detailed explanation of R² can be found in the section: R² Coefficient of Determination

Alternative Algorithms

While decision tree regression is easy to understand and interpret, other algorithms can offer better performance, especially in complex or noisy datasets.

Random Forest: Random Forest is an ensemble learning method that builds multiple decision trees and averages their predictions to improve accuracy. By aggregating results from diverse trees, it reduces overfitting and increases model stability. However, it is less interpretable than a single decision tree and requires more computational resources. Learn more
Linear Regression: Linear Regression models the relationship between input features and the target using a straight-line equation. It is fast, easy to implement, and works well when the underlying relationship is linear. However, it struggles with non-linear patterns and is sensitive to outliers and certain statistical assumptions. Learn more
Support Vector Regression: Support Vector Regression fits a function within a margin of tolerance from the actual data points, using support vectors to define the model. It is effective for modeling both linear and non-linear relationships, especially on smaller datasets. The downside is that it's computationally intensive on large datasets and requires careful tuning. Learn more
k-Nearest Neighbors (k-NN): k-NN regression predicts a value by averaging the outputs of the k most similar data points in the training set. It's simple, intuitive, and requires no explicit training phase. However, it can be slow on large datasets and sensitive to irrelevant features and noise. Learn more
Gradient Boosting (XGBoost, LightGBM): Gradient Boosting builds decision trees sequentially, with each new tree correcting the errors of the previous ones. It delivers high accuracy and handles complex, non-linear patterns effectively. On the downside, it tends to be slower to train and demands careful hyperparameter tuning.

Advantages and Disadvantages

Decision tree regression offers a number of benefits, especially in terms of simplicity and interpretability, but it also comes with limitations that are important to consider depending on your use case.

✅ Advantages:

The model's structure mimics human decision-making and can be visualized as a flowchart, making it intuitive.
No need to normalize features or create dummy variables. Trees handle both numerical and categorical features naturally.
Decision trees can model complex interactions between features without needing to manually specify them.
Training is typically fast and straightforward without requiring heavy computational resources.

❌ Disadvantages:

A single decision tree may fit the training data too closely, especially if it is deep, leading to poor generalization on unseen data.
Slight changes in the dataset can lead to a completely different tree structure.
Other models like random forests or gradient boosting typically achieve better predictive performance.
While trees can capture non-linear patterns, a single tree might still struggle with very high-dimensional or noisy data.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🟡 Medium

Use Case Examples

Real Estate Price Prediction

Predicting the selling price of a house based on features such as square footage, number of bedrooms, location, and age of the property.

Forecasting Electricity Demand

Used by utility companies to estimate future energy consumption based on variables like time of day, temperature, and historical usage data.

Agricultural Yield Estimation

Helps predict crop yields based on weather patterns, soil quality, irrigation levels, and planting practices.

Insurance Risk Assessment

Estimating claim costs or insurance premiums by analyzing customer data, past claims, and risk factors.

Manufacturing Quality Control

Predicting the expected strength or durability of a product based on material properties and production conditions.

Conclusion

Decision tree regression is a simple yet powerful algorithm for predicting continuous numerical values. It works by recursively splitting the data into smaller regions where the target values are more uniform, and it makes predictions based on the average of these regions. Its biggest strengths lie in its ease of understanding, flexibility in handling different types of data, and ability to model non-linear relationships. It's especially useful in domains where model interpretability is important, such as finance, healthcare, and engineering.

However, decision tree regression also has limitations. It tends to overfit if not properly controlled and is sensitive to small changes in the data. For more accurate and stable predictions, especially in complex tasks, ensemble methods like random forests or gradient boosting are often preferred.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.