Random Forest

Machine Learning → Supervised Learning → Classification → Single Label Classification → Multi Class Classification

Random Forest is a machine learning algorithm that belongs to the category of supervised learning. This algorithm is primarily used for prediction and classification of data. The basic idea is that it combines the predictions of many decision trees, thereby reducing the risk of overfitting and increasing the model's accuracy. It is used to solve problems where we need to predict outputs based on historical data, such as classification as well as regression. It is effective for predictions where the data is diverse and contains a large number of different variables.

How It Works

The Random Forest algorithm is essentially an ensemble of decision trees. These trees are trained independently on different subsets of the data, and their results are then combined to produce the final prediction.

Decision Trees

A decision tree is a model used to predict an output based on a series of decisions. Each node in the tree represents a question about a data feature, and each leaf node represents a prediction (e.g., a class or a value).

Let’s imagine we have a dataset of customers and we want to predict whether a customer will buy a product:

First node: "Is the customer over 30 years old?"

Yes: go to the next node.
No: go to the leaf "Will buy product: no".

Second node: "Does the customer have a monthly income higher than €2000?"

Yes: go to the leaf "Will buy product: yes".
No: go to the leaf "Will buy product: no".

This process continues until a final answer is reached. Each decision tree thus searches for a path of decisions that best predicts the output.

Ensemble Method: Forest

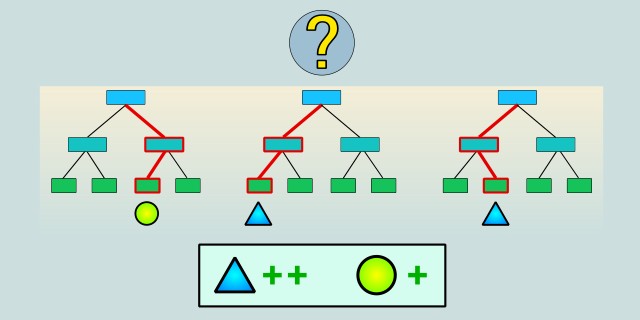
Random Forest is a “forest” of decision trees, meaning that instead of using a single decision tree, we use an entire collection of trees. Combining multiple trees reduces the risk of overfitting and improves the model’s stability. Since each tree is trained on a different sample of the data and selects random subsets of features, the final model can generalize better than a single tree. A key factor is that Random Forest uses randomness to avoid errors that might arise if the model were trained on just one decision tree.

The algorithm randomly selects a subset of data from the input dataset using a technique called bootstrapping (random sampling with replacement). Each decision tree is therefore trained on a different sample of the data.

When building each tree, random subsets of features (attributes) are also selected to determine the best splits at each node. This randomized approach increases the diversity of the trees and helps prevent overfitting.

After training all the trees, the algorithm combines their predictions to produce a final result. In classification, this can be a majority vote among the trees (i.e., the class predicted by most trees), and in regression, it is typically the average of all the trees’ predictions.

Mathematical Foundation

Random Forest is based on several mathematical principles, the most important of which include improving generalization through the ensemble method, data splitting criteria (such as the Gini index and entropy), and the random selection of samples and features during tree training.

Ensemble Method

Random Forest is an ensemble algorithm, meaning it combines multiple models (decision trees). The goal is to reduce prediction variance and improve stability.

Mathematically, the prediction $\hat{y}$ can be expressed as:

$$\hat{y} = \frac{1}{N} \sum_{i=1}^{N} f_i(x)$$

$N$ is the number of trees in the forest (ensemble).
$f_i(x)$ is the prediction of the $i$-th tree for the input $x$.

In the case of classification, the final prediction is the majority vote among all trees. For regression, it is the average of all tree predictions.

Training Decision Trees

Each tree is trained using random samples from the input dataset (bootstrapping) and a random selection of features. The goal is to ensure that each tree is sufficiently diverse, minimizing the risk of overfitting.

Bootstrapping:

Bootstrapping is a technique in which a random subset $D'$ is created from the original dataset $D$ with replacement. That means some examples may appear more than once, while others may be left out entirely. Each tree is trained on a slightly different version of the data, which increases robustness.

Feature Selection:

For each node in the tree, a random subset $m$ of the total number of features $p$ is selected, from which the best split is chosen. This process can be described mathematically as selecting the best split based on a splitting criterion.

Splitting Criteria

When building decision trees, a decision must be made at each node about how to split the data. The most commonly used methods are the Gini index and entropy. The Gini index measures the purity of the split at a node.

It is defined as:

$$Gini(t) = 1 - \sum_{i=1}^{C} p_i^2$$

$t$ is the node.
$C$ is the number of classes in the data.
$p_i$ is the probability that a random point belongs to class $i$.

A lower Gini index means a "purer" split, i.e., most of the data at that node belongs to a single class.

Entropy measures the uncertainty or disorder of data in a node.

It is defined as:

$$H(t) = - \sum_{i=1}^{C} p_i \log_2 p_i$$

$p_i$ is the probability of class $i$ at the node.

A lower entropy means a "purer" split, similar to the Gini index.

Overfitting and Generalization

One of the advantages of Random Forest is that even though each individual tree may be prone to overfitting (especially if trained on the entire dataset), combining multiple trees results in a more stable model. This process reduces model variance, leading to better generalization.

Mathematically, this stabilization can be seen in the reduction of model variance.

For an individual tree $f_i(x)$:

$$\text{Var}(f(x)) = \frac{1}{N} \sum_{i=1}^{N} \text{Var}(f_i(x))$$

By using the ensemble approach, where the trees "compensate" for one another, the overall variance is reduced, resulting in more accurate and robust predictions.

Code Example

A basic implementation that includes generating random data (as a dataset), building decision trees, and combining predictions from multiple trees.

use rand::Rng;              // For generating random numbers

#[derive(Debug, Clone)]
struct DecisionTree {
    // The tree will represent a simple structure with a split criterion
    feature_index: usize,
    threshold: f64,
    left: Option<Box<DecisionTree>>,
    right: Option<Box<DecisionTree>>,
    prediction: Option<u32>,  // Class prediction
}

impl DecisionTree {
    // Create a new decision tree
    fn new(feature_index: usize, threshold: f64) -> Self {
        DecisionTree {
            feature_index,
            threshold,
            left: None,
            right: None,
            prediction: None,
        }
    }

    // Function for prediction using the tree
    fn predict(&self, sample: &Vec<f64>) -> u32 {
        if let Some(pred) = self.prediction {
            return pred;
        }

        if sample[self.feature_index] <= self.threshold {
            match &self.left {
                Some(left_tree) => left_tree.predict(sample),
                None => 0, // Default class if left branch is missing
            }
        } else {
            match &self.right {
                Some(right_tree) => right_tree.predict(sample),
                None => 1, // Default class if right branch is missing
            }
        }
    }

    // Function for "training" the tree (very simplified)
    fn train(&mut self, data: &Vec<Vec<f64>>, labels: &Vec<u32>) {
        // Stopping condition: if all labels are the same, make this a leaf node
        if labels.iter().all(|&l| l == labels[0]) {
            self.prediction = Some(labels[0]);
            return;
        }
        // Stopping condition: if data is empty or only one sample, make this a leaf node with the most common label
        if data.is_empty() || data.len() == 1 {
            let mut counts = [0, 0];
            for &l in labels {
                if l < 2 { counts[l as usize] += 1; }
            }
            let majority = if counts[0] >= counts[1] { 0 } else { 1 };
            self.prediction = Some(majority);
            return;
        }

        let mut rng = rand::thread_rng();
        let index = rng.gen_range(0..data[0].len());  // Select a random attribute
        let threshold = data.iter().map(|x| x[index]).sum::<f64>() / data.len() as f64;  // Simplified criterion for threshold

        self.feature_index = index;
        self.threshold = threshold;

        let (left_data, left_labels, right_data, right_labels) = self.split_data(data, labels, index, threshold);

        // If either split is empty, make this a leaf node with the most common label
        if left_data.is_empty() || right_data.is_empty() {
            let mut counts = [0, 0];
            for &l in labels {
                if l < 2 { counts[l as usize] += 1; }
            }
            let majority = if counts[0] >= counts[1] { 0 } else { 1 };
            self.prediction = Some(majority);
            return;
        }

        self.left = Some(Box::new(DecisionTree::new(index, threshold)));
        self.right = Some(Box::new(DecisionTree::new(index, threshold)));

        // Recursively train trees for the left and right branches
        self.left.as_mut().unwrap().train(&left_data, &left_labels);
        self.right.as_mut().unwrap().train(&right_data, &right_labels);
    }

    // Split data according to the threshold
    fn split_data(&self, data: &Vec<Vec<f64>>, labels: &Vec<u32>, feature_index: usize, threshold: f64) -> (Vec<Vec<f64>>, Vec<u32>, Vec<Vec<f64>>, Vec<u32>) {
        let mut left_data = Vec::new();
        let mut left_labels = Vec::new();
        let mut right_data = Vec::new();
        let mut right_labels = Vec::new();

        for i in 0..data.len() {
            if data[i][feature_index] <= threshold {
                left_data.push(data[i].clone());
                left_labels.push(labels[i]);
            } else {
                right_data.push(data[i].clone());
                right_labels.push(labels[i]);
            }
        }

        (left_data, left_labels, right_data, right_labels)
    }
}

// Function for training Random Forest
fn train_random_forest(data: Vec<Vec<f64>>, labels: Vec<u32>, num_trees: usize) -> Vec<DecisionTree> {
    let mut forest = Vec::new();
    
    for _ in 0..num_trees {
        let mut tree = DecisionTree::new(0, 0.0);
        tree.train(&data, &labels);
        forest.push(tree);
    }

    forest
}

// Prediction with Random Forest
fn predict_forest(forest: &Vec<DecisionTree>, sample: &Vec<f64>) -> u32 {
    let mut votes = vec![0, 0]; // Count votes for each class
    for tree in forest {
        let prediction = tree.predict(sample);
        votes[prediction as usize] += 1;
    }

    // Return the class with the highest number of votes
    if votes[0] > votes[1] { 0 } else { 1 }
}

fn main() {
    // Example data and labels
    let data = vec![
        vec![2.7, 1.5],  // Example 1
        vec![1.2, 3.4],  // Example 2
        vec![3.1, 4.5],  // Example 3
        vec![4.6, 2.1],  // Example 4
    ];
    let labels = vec![0, 1, 1, 0];  // Target labels for each example

    // Training Random Forest with 3 trees
    let forest = train_random_forest(data.clone(), labels.clone(), 3);

    // Prediction for a new example
    let new_sample = vec![3.0, 2.0];
    let prediction = predict_forest(&forest, &new_sample);
    println!("Prediction for new example: {}", prediction);
}

DecisionTree struct: This structure represents a decision tree. It contains the feature index, a threshold for splitting, the left and right branches, and the predicted class.
Training the tree: The train method trains the tree based on the data, randomly selecting an attribute and using a very simplified threshold selection for splitting. Data samples are then divided into the left and right branches.
Random Forest: The train_random_forest function trains multiple trees and returns a vector of all trees (the Random Forest).
Prediction: The predict_forest function aggregates predictions from all trees. Each tree casts a vote, and the final prediction is the one with the most votes.

Model Evaluation for Classification

Model evaluation depends on the type of task being solved. Whether it's classification or regression, it's important to measure how well the model predicts outcomes. For classification tasks (where the model predicts a category or class), we can use metrics such as accuracy, precision, recall, F1 score, or a confusion matrix.

Accuracy

Accuracy is the most basic metric that shows the proportion of correct predictions out of the total number of predictions. It indicates what fraction of all predictions the model identified correctly.

$$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total number of predictions}}$$

If the dataset is imbalanced (e.g., 95% of class 0), accuracy can be misleading.

Accuracy of 90% or higher is generally considered good for balanced and noise-free datasets.

👉 A detailed explanation of Accuracy can be found in the section: Accuracy

Precision

Precision tells us how many of the predicted positive results were actually correct. It is important when avoiding false positives is critical (for example, in medicine where a wrong diagnosis can have serious consequences).

$$\text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}$$

Important when false positives are problematic (e.g., labeling a valid email as spam, or medicine diagnostics).

👉 A detailed explanation of Precision can be found in the section: Precision

Recall (Sensitivity)

Recall tells us how many of the actual positive cases the model correctly identified. It is important when minimizing false negatives is necessary, i.e., situations where the model misses real positive cases (for example, in cancer detection, where failing to detect a positive case can be dangerous).

$$\text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}$$

Important when false negatives are problematic (e.g., missing a disease diagnosis).

👉 A detailed explanation of Recall can be found in the section: Recall

F1 Score

The F1 score is the harmonic mean of precision and recall. It is very useful when both precision and recall need to be balanced. This metric is valuable when we want to consider both the correctness of positive predictions and the ability to find all actual positive cases.

$$\text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$

Especially useful for imbalanced class distributions.

F1 score of 0.8 or higher is generally considered good.

👉 A detailed explanation of F1 Score can be found in the section: F1 Score

Confusion Matrix

A confusion matrix is a table that summarizes the performance of a classification model by showing the counts of true positives, false positives, true negatives, and false negatives. It provides a detailed breakdown of how the model’s predictions compare to the actual labels and helps identify specific types of errors.

	Predicted Positive	Predicted Negative
Actual Positive	TP	FN
Actual Negative	FP	TN

TP (True Positives) – Correctly predicted positive cases.
TN (True Negatives) – Correctly predicted negative cases.
FP (False Positives) – Incorrectly predicted positive cases.
FN (False Negatives) – Incorrectly predicted negative cases.

Model Evaluation for Regression

For regression tasks (where the model predicts a numerical value), we can use metrics such as MAE, MSE, or R².

MAE (Mean Absolute Error)

Mean Absolute Error (MAE) is a metric used to evaluate regression models by measuring the average absolute difference between actual and predicted values. MAE treats all errors equally, making it more robust to outliers and noise in the data.

It represents the average absolute difference between the actual and predicted values:

$$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$

👉 A detailed explanation of MAE can be found in the section: Mean Absolute Error

MSE (Mean Squared Error)

MSE penalizes larger errors more than smaller ones (because the error is squared).

It represents the average squared difference between the actual and predicted values:

$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$

👉 A detailed explanation of MSE can be found in the section: Mean Squared Error

RMSE (Root Mean Squared Error)

RMSE has the same units as the original values, making it more intuitive to interpret.

It represents the average squared difference between the actual and predicted values:

$$ \text{RMSE} = \sqrt{\text{MSE}} $$

👉 A detailed explanation of RMSE can be found in the section: Root Mean Squared Error

R² (Coefficient of Determination)

R² indicates how much of the variability in the data can be explained by the model:

$$ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} $$

Close to 1 – the model explains the variability in the data very well.
Close to 0 – the model explains very little of the variability.

👉 A detailed explanation of R² can be found in the section: R² Coefficient of Determination

Alternative Algorithms

There are several algorithms suitable for both classification and regression tasks, similar to Random Forest. Each of these algorithms has its own advantages and disadvantages depending on the nature of the problem, data characteristics, and performance requirements.

Gradient Boosting Machines (GBM): Gradient Boosting is often considered a strong alternative to Random Forest. While Random Forest trains multiple independent trees and combines their predictions, Gradient Boosting trains trees sequentially, with each new tree attempting to correct the errors of the previous ones.
K-Nearest Neighbors (k-NN): K-Nearest Neighbors (k-NN) is a simple yet effective algorithm for both classification and regression. It does not involve an explicit training process; instead, it makes predictions based on the closest neighbors in the training dataset. Learn more
Neural Networks: Neural networks are suitable for various tasks, including classification and prediction. These networks consist of layers that transform input data into output through weights and activation functions. Models like CNNs (Convolutional Neural Networks) and RNNs (Recurrent Neural Networks) are used in specialized applications.

Advantages and Disadvantages

Random Forest is a useful algorithm for many machine learning problems, particularly due to its robustness against overfitting, flexibility, and low requirement for data preprocessing. It is well-suited for tasks where reliability and robustness are essential, especially in cases of imbalanced or noisy data. However, its computational cost, low interpretability, and high memory usage can be drawbacks in certain applications.

✅ Advantages:

Robustness against overfitting.
Flexibility, can be used for both classification and regression.
Low need for data preprocessing.
Parallelization, each tree can be trained independently.

❌ Disadvantages:

High computational cost.
Low interpretability.
High memory usage.
Less effective with extremely imbalanced datasets.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🟡 Medium

Use Case Examples

Heart Disease Prediction (Classification)

Random Forest is commonly used to predict the risk of various diseases, such as heart attacks or other cardiovascular conditions, based on input data such as age, gender, blood pressure, cholesterol level, and more. This is a classification problem where the target variable is binary (e.g., "Is the patient at risk of heart disease?").

Fraud Detection in Banking (Classification)

In banking, detecting fraudulent transactions is critical. Random Forest can be used to classify transactions as "normal" or "fraudulent" based on various features such as transaction amount, location, time, frequency, customer history, and so on.

Manufacturing Defect Prediction (Classification)

In industrial applications, Random Forest is used to predict product defects during the manufacturing process. Based on data from production parameters (temperature, pressure, line speed, material, etc.), Random Forest can help identify the risk of defects in the production line.

Wine Quality Prediction (Regression)

Random Forest can be used to predict wine quality based on various chemical properties such as acidity, pH, sugar content, alcohol level, and more. This problem is a typical example of regression, where the target variable (wine quality) is numerical, and Random Forest can capture complex patterns in the data to effectively predict the outcome.

Product Sales Forecasting (Regression)

In retail, models are often used to forecast product sales based on factors such as seasonality, pricing, demand, marketing campaigns, and more. Random Forest can predict which products will have the highest demand during specific periods.

Conclusion

Random Forest is a machine learning algorithm that finds wide application across various fields such as healthcare, finance, industrial manufacturing, and commerce. Its strengths, including robustness against overfitting, the ability to handle diverse data types, and model complex patterns, make it an ideal tool for a broad range of tasks.

However, although Random Forest is a powerful model, it is not without drawbacks. It requires significant computational and memory resources, especially with large datasets, and can be less interpretable compared to simpler models. This may pose challenges in applications where decision-making transparency is crucial, such as in medicine or law.

For problems involving large, noisy datasets where robustness and the ability to handle non-linear patterns are essential, Random Forest is an excellent choice. If you decide to use it, be sure to properly tune the hyperparameters and evaluate the model using appropriate metrics to achieve the best performance.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.