DBSCAN

Machine Learning → Unsupervised Learning → Clustering

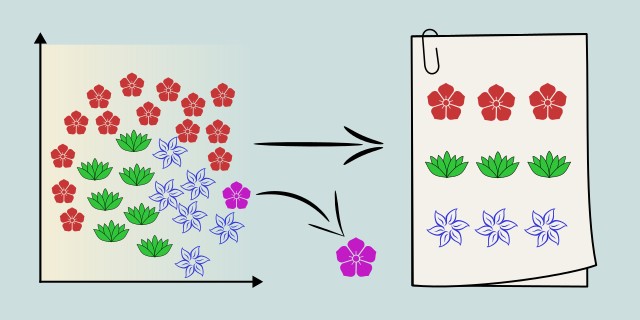
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is an unsupervised machine learning algorithm used for clustering tasks. Unlike traditional clustering techniques such as K-Means, DBSCAN does not require the number of clusters to be specified in advance, and it can find clusters of arbitrary shape and size.

DBSCAN is particularly effective in identifying clusters in data that contains noise or outliers. It groups together points that are closely packed (points with many nearby neighbors), and marks as outliers the points that lie alone in low-density regions. Its strength lies in its ability to discover non-linear cluster boundaries and to work well without much domain-specific preprocessing.

How It Works

DBSCAN is a clustering algorithm that groups data points based on density. This means how close the points are to each other in feature space. Instead of assuming how many clusters exist (as K-Means does), DBSCAN explores the data and finds dense areas, treating everything else as noise or outliers.

The algorithm is based on two key parameters:

$\epsilon$ (epsilon): the radius of a neighborhood around a point.
minPts: the minimum number of points required to form a dense region (i.e., a cluster).

Example

Let's imagine that we are analyzing a city map with dots representing café locations. Your goal is to identify popular café zones (where many cafés are clustered together), and ignore isolated cafés that don’t belong to any group.

Let's agree on the parameters:

A popular zone is where at least 4 cafés are located within a few blocks of each other (this is your 'minPts').
A café is considered "nearby" if it’s within a 500-meter radius (this is your $\epsilon$ or epsilon).

1. Start with an unvisited point

Pick a random café (let’s say "Café A") that hasn’t been checked yet.

2. Check its neighborhood

Draw a circle with a 500-meter radius around Café A. Count how many other cafés are within that circle, including Café A itself.

3. Classify the point

There are three possible outcomes:

Core Point: If there are 4 or more cafés (including Café A) inside the circle, then Café A is a core point; the beginning of a potential cluster.
Border Point: If there are fewer than 4 cafés, but Café A is still within range of a core point, it’s a border point; part of a cluster but not dense enough to start one itself.
Noise Point: If there are fewer than 4 cafés and Café A is not close to any core point, it’s labeled noise; an outlier.

4. Expand the cluster

If Café A is a core point:

Add all neighboring cafés (within 500 meters) to the same cluster.
For each of those neighbors, check if **they** are core points.
If they are, repeat the process: check their neighbors, and expand the cluster outward.
This continues until no more points can be added to this cluster.

5. Move on

Mark all cafés in this cluster as “visited”.
Pick another unvisited point and repeat steps 1–4.
Keep repeating until all cafés are either part of a cluster or labeled as noise.

In summary, DBSCAN builds clusters by connecting points that are closely packed together, while labeling points in sparse regions as noise. It’s like following a trail of breadcrumbs: if there are enough crumbs close together, it counts as a pile (cluster); otherwise, they’re just scattered crumbs (noise).

Mathematical Foundation

DBSCAN groups data points that are closely packed together and separates regions of low point density.

It uses two parameters:

$\epsilon$ (epsilon): the radius of a neighborhood around a point.
minPts: the minimum number of points required to form a dense region (i.e., a cluster).

Plot the k-distance graph (typically with $k = \text{minPts} - 1$) and look for the "elbow" to choose a good $\epsilon$ value. Larger $\epsilon$ may lead to merging clusters; smaller $\epsilon$ may lead to fragmented clusters or too many noise points.

Set minPts ≥ dimensionality of data + 1 (e.g., 3D data → minPts ≥ 4). Higher minPts increases the minimum density required for forming a cluster.

Key Definitions

ε-Neighborhood

For a point $p$, the ε-neighborhood is defined as:

$$N_\varepsilon(p) = \{q \in D \mid \text{distance}(p, q) \leq \varepsilon\}$$

$D$ is the dataset.
$\text{distance}(p, q)$ is typically Euclidean distance between $p$ and $q$.
This is the set of all points within a distance $\varepsilon$ of point $p$.

Core Point

A point $p$ is a core point if:

$$|N_\varepsilon(p)| \geq \text{minPts}$$

That is, there are at least `minPts` points in its ε-neighborhood (including the point itself).

Border Point

A point $p$ is a border point if:

It is not a core point (i.e., $|N_\varepsilon(p)| < \text{minPts}$).
It is within the ε-neighborhood of a core point.

Border points are part of a cluster but do not have enough neighbors to be core points themselves.

Noise Point (Outlier)

A point that is neither a core point nor a border point is labeled as noise.

Density Reachability and Connectivity

These two concepts allow DBSCAN to grow clusters from core points.

Directly Density-Reachable

A point $p$ is directly density-reachable from $q$ if:

$p \in N_\varepsilon(q)$.
$q$ is a core point.

Density-Reachable

A point $p$ is density-reachable from $q$ if there is a chain of points $p_1, p_2, ..., p_n$ such that:

$$p_1 = q,\quad p_n = p,\quad \text{and each } p_{i+1} \text{ is directly density-reachable from } p_i$$

Density-reachability is not symmetric, just because $p$ is reachable from $q$, does not mean $q$ is reachable from $p$.

Density-Connected

Two points $p$ and $q$ are density-connected if there exists a point $o$ such that both $p$ and $q$ are density-reachable from $o$.

This forms the basis for clusters: a cluster is a set of points that are all density-connected.

Distance Metric

DBSCAN typically uses Euclidean distance, defined for points $p = (p_1, p_2, ..., p_n)$ and $q = (q_1, q_2, ..., q_n)$ as:

$$\text{distance}(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + \ldots + (p_n - q_n)^2}$$

However, other distance metrics (e.g., Manhattan, Haversine) can be used depending on the data.

Code Example

We’ll implement DBSCAN clustering in Rust using the linfa machine learning library. We’ll use a simple synthetic 2D dataset of points grouped in clusters to demonstrate how DBSCAN identifies those clusters and labels outliers.

Dependencies

To run this code, make sure you add the following dependencies in your Cargo.toml:

[dependencies]
linfa = "0.6.1"
linfa-clustering = "0.6.1"
ndarray = "0.15"

Code

use linfa::traits::Transformer;
use linfa_clustering::Dbscan;
use ndarray::array;

fn main() {
    // Step 1: Create a simple dataset of 2D points (x, y)
    let data = array![
        [1.0, 2.0],
        [1.1, 2.1],
        [0.9, 1.9],
        [8.0, 8.0],
        [8.1, 8.1],
        [8.2, 7.9],
        [25.0, 80.0] // This one is a noise point (outlier)
    ];

    // Step 2: Define DBSCAN parameters
    // eps = 0.5: neighborhood radius
    // min_points = 2: minimum neighbors to form a dense region
    let dbscan = Dbscan::params(2)
        .tolerance(0.5)
        .transform(&data)
        .expect("DBSCAN clustering failed");

    // Step 3: Print results
    println!("Cluster assignments:");
    for (i, cluster) in dbscan.iter().enumerate() {
        match cluster {
            Some(label) => println!("Point {} is in cluster {}", i, label),
            None => println!("Point {} is noise", i),
        }
    }

    // Optional: Print the number of clusters found
    use std::collections::HashSet;
    let n_clusters = dbscan.iter().filter_map(|&x| x).collect::<HashSet<_>>().len();
    println!("Total clusters found: {}", n_clusters);
}

Output

This shows two clear clusters and one point (far from others) marked as noise.

Cluster assignments:
Point 0 is in cluster 0
Point 1 is in cluster 0
Point 2 is in cluster 0
Point 3 is in cluster 1
Point 4 is in cluster 1
Point 5 is in cluster 1
Point 6 is noise
Total clusters found: 2

Model Evaluation

Evaluating the quality of clustering is a bit different from evaluating supervised models because there are no ground-truth labels in most unsupervised learning scenarios. However, if we have actual values available (e.g., in reference datasets), we can use external metrics. If we don't have them, we rely on internal metrics that evaluate the structure of the clustering itself.

Silhouette Score (Internal)

Evaluates how similar each point is to its own cluster vs. others, after “cutting” the dendrogram into flat clusters. It ranges from -1 to 1:

$$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$$

$a(i)$: mean intra-cluster distance (how close point $i$ is to others in its own cluster).
$b(i)$: mean nearest-cluster distance (how close point $i$ is to points in the nearest different).

A score close to 1 means the point is well matched to its cluster.
A score near 0 means the point lies between two clusters.
A negative score indicates potential misclassification.

After segmenting customers, a high average silhouette score means most customers clearly belong to one group.

Davies–Bouldin Index (Internal)

The Davies–Bouldin Index measures intra-cluster similarity and inter-cluster difference. Lower values are better:

It compares the distance between cluster centroids to the size (spread) of the clusters.
A score close to 0 indicates well-separated, tight clusters.

Dunn Index (Internal)

Measures the ratio between the minimum inter-cluster distance and the maximum intra-cluster distance.

$$\text{Dunn} = \frac{\min(\text{distance between clusters})}{\max(\text{cluster diameter})}$$

Higher values indicate better clustering.

Adjusted Rand Index (External)

Measures how similar the clustering is to the ground truth. Adjusts for chance grouping.

Range: -1 to 1

1: perfect match.
0: random clustering.
Negative: worse than random.

Normalized Mutual Information (External)

Measures mutual dependence between predicted clusters and ground-truth labels.

$$\text{NMI} = \frac{2 \cdot I(X; Y)}{H(X) + H(Y)}$$

$I(X; Y)$ is mutual information.
$H(X), H(Y)$ are the entropies of the clusters.

Range: 0 (no mutual info) to 1 (perfect correlation)

Alternative Algorithms

Hierarchical Clustering: Hierarchical clustering builds a tree-like structure of clusters and doesn’t require the number of clusters to be specified upfront. It's ideal for small datasets with nested relationships but is sensitive to noise and computationally expensive for large datasets. Learn more
k-Means: K-Means divides data into clusters by minimizing distances to centroids, making it fast and efficient for large, well-separated datasets. However, it requires pre-specifying the number of clusters and struggles with noise, outliers, or clusters of varying shapes and sizes. Learn more
Mean Shift:Mean Shift identifies clusters by shifting data points toward high-density areas. It doesn’t need the number of clusters specified but can be computationally expensive and may struggle in high-dimensional spaces, with results sensitive to the bandwidth parameter.
OPTICS: OPTICS extends DBSCAN by handling clusters with varying densities and maintaining the ability to detect noise, without needing a global epsilon value. It's more complex and slower than DBSCAN but useful when cluster densities are non-uniform.
Gaussian Mixture Models (GMM): GMM models data as a combination of Gaussian distributions and allows soft clustering, providing probabilities for cluster assignments. It requires knowledge of the number of clusters and assumes a Gaussian distribution, making it ideal for probabilistic applications but sensitive to initialization.

Advantages and Disadvantages

DBSCAN is a powerful clustering algorithm that offers several advantages, such as automatically determining the number of clusters and handling irregular or non-linear cluster shapes. It is particularly useful for messy, real-world data and requires minimal parameters, making it user-friendly. However, its performance can be sensitive to the choice of parameters like ε, and it struggles with varying densities across clusters or high-dimensional data, limiting its scalability and flexibility in certain scenarios.

✅ Advantages:

Unlike K-Means or GMM, DBSCAN automatically determines the number of clusters based on data density.
Method is not limited to convex or spherical clusters, it handles irregular, non-linear cluster boundaries well.
Points that don’t fit into any dense region are labeled as noise, making the algorithm suitable for real-world, messy data.
Its density-based approach is particularly suited for detecting clusters in geographic, sensor, or social network data.
Only two parameters (ε and minPts) are required, and they are often easier to interpret than other hyperparameters.

❌ Disadvantages:

The clustering outcome can change significantly with small variations in these parameters, especially ε.
DBSCAN assumes a uniform density across clusters. It may merge nearby clusters or split one cluster into many if densities differ.
As dimensionality increases, distance metrics become less meaningful, which reduces clustering quality.
While scalable, DBSCAN can be less efficient or accurate than model-based or hierarchical approaches on very large or complex datasets.
Unlike Gaussian Mixture Models, DBSCAN assigns each point to a single cluster or noise, without confidence scores or soft labels.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🔴 High

Use Case Examples

Geospatial Analysis: Identifying Hotspots

In urban planning or transportation, DBSCAN is used to find high-density regions of interest. Detecting clusters of taxi pickup and drop-off locations in a city.

Anomaly Detection in Network Security

DBSCAN is applied to detect abnormal activity that deviates from normal patterns. Identifying unusual login locations or traffic spikes in network logs.

Astronomy: Galaxy and Star Clustering

Astronomers use DBSCAN to analyze celestial data. Grouping stars or galaxies based on their spatial proximity and brightness.

Retail and Marketing: Customer Segmentation

Businesses analyze customer behavior to personalize services. Segmenting customers based on location and shopping patterns.

Image Processing: Object Detection

In computer vision, DBSCAN helps identify objects or boundaries. Detecting groups of pixels in satellite imagery or biological cells in microscopy.

Conclusion

DBSCAN is an intuitive clustering algorithm that excels in scenarios where data is noisy, irregularly shaped, or where the number of clusters is unknown. Its ability to automatically discover clusters of varying shape and mark outliers makes it a valuable tool in many practical applications.

While DBSCAN isn’t a one-size-fits-all solution, its simplicity, robustness to noise, and lack of requirement for predefined cluster count make it a strong candidate in many real-world unsupervised learning tasks.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.