Support Vector Machine

Machine Learning → Supervised Learning → Classification → Single Label Classification → Binary Classification

Support Vector Machines (SVM) is a machine learning algorithm used for classification and regression. In this context, the focus will primarily be on its use in binary classification. SVM is often applied to tasks where the goal is to find the optimal boundary between different classes of data, such as in binary classification problems (e.g., spam vs. not spam). It focuses on finding the best possible boundary (called a hyperplane) between two classes of data. It is also effective for both linear and non-linear problems (using kernels). It is most commonly used in cases where the goal is to distinguish between two classes.

How It Works

Support Vector Machine (SVM) is an algorithm primarily used for binary classification, meaning it tries to separate data into two classes. It aims to find the best possible boundary (hyperplane) that separates these two classes. This process of finding the boundary is called training the model.

Linear Data

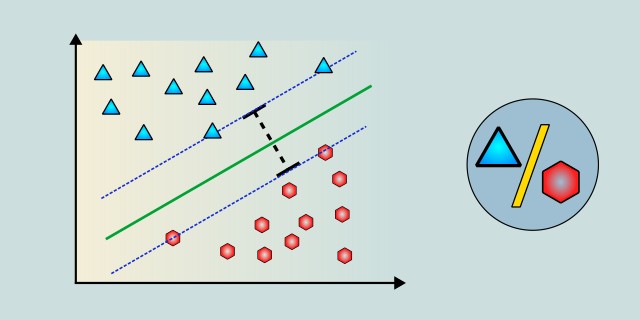
Imagine we have a dataset with points on a 2D plane, where each point belongs either to class A (blue) or class B (red). The goal is to find the equation of a line (in 2D) that separates these two classes. At first glance, we might see several different lines that could separate these points, but SVM focuses on finding the line that maximizes the margin. The margin is the distance between the separating boundary (line in 2D, hyperplane in n-D) and the closest points from each class. These closest points are called Support Vectors. These points are important because they define the boundary.

SVM tries to maximize this margin so that the model generalizes as much as possible. A larger margin means a better ability of the model to generalize to new, unseen data. If the margin is very small, the model might be too fitted to the training data (overfitting), which can worsen its performance on test data.

Non-linear Data

Not all data are linearly separable. This means we cannot simply draw a line (or hyperplane) that perfectly separates both classes. In such cases, the Kernel trick is used. The Kernel trick is a technique that allows transforming data into a higher dimension where they can be linearly separable. This process does not require explicitly computing new features (which would be computationally expensive) because SVM uses kernel functions that allow the model to work in this higher dimension.

We can imagine points that are not separable by a line (for example, point A in the center and point B around it in a circular shape). By using a polynomial or Gaussian kernel (RBF kernel), we can transform this data into a higher dimension (e.g., 3D space) where it can be easily separated by a plane.

Optimization

SVM tries to find the best separating boundary, but it is not as simple as it seems at first glance. SVM has several hyperparameters that need to be tuned to achieve the best performance.

C (penalty parameter): This parameter controls the trade-off between maximizing the margin and minimizing the error on training data. If C is very high, the model will try to perfectly separate all data (which can lead to overfitting). If C is too low, the model may be too tolerant of errors.
Kernel: Choosing the right kernel (e.g., linear, polynomial, RBF) is very important for the model to work properly, especially in non-linear problems.
Gamma $\gamma$: This parameter determines how much influence each training point has on creating the decision boundary. A higher gamma value can cause the model to be very sensitive to noise in the data, leading to overfitting.

Mathematical Foundation

Linear Separation

Imagine we have a dataset that is linearly separable. This means there exists a line (in 2D) or a hyperplane (in n-D) that can separate the data into two classes. The goal of SVM is to find such a line (hyperplane) that maximizes the margin; the distance between the closest points from each class and the boundary itself.

Suppose the data are divided into two classes, $C_1$ and $C_2$, and we want to find the line that best separates these classes.

Mathematically, the separating line can be expressed as:

$$\mathbf{w} \cdot \mathbf{x} + b = 0$$

$\mathbf{w}$ is the weight vector that determines the orientation of the separating line.
$\mathbf{x}$ is the input data vector (a point in space).
$b$ is the bias, which shifts the line.

SVM searches for the line that maximizes the margin between the closest points of each class. To maximize the margin, the norm of the vector $\mathbf{w}$ is minimized, which means SVM tries to find optimal values of $\mathbf{w}$ and $b$.

The margin is defined as:

$$\text{margin} = \frac{1}{\|\mathbf{w}\|}$$

The points that lie on the edge of the margin are called support vectors. These points are crucial in determining the separating boundary, because if we removed them, the boundary would change.

For points in class $C_1$, the condition is:

$$\mathbf{w} \cdot \mathbf{x}_i + b \geq 1 \quad \text{for all } \mathbf{x}_i \in C_1$$

And for class $C_2$:

$$\mathbf{w} \cdot \mathbf{x}_i + b \leq -1 \quad \text{for all } \mathbf{x}_i \in C_2$$

This system of two constraints ensures all points are correctly classified while the separating boundary is as far as possible from these points, thus maximizing the margin.

Optimization Problem

The goal is to find values of $\mathbf{w}$ and $b$ that maximize the margin, which is equivalent to minimizing $\|\mathbf{w}\|^2$.

This problem can be formulated as:

$$\min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2$$

Subject to the constraints for each class:

$$y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 \quad \text{for all } i$$

Where $y_i$ is the target variable (+1 or -1 depending on which class the point belongs to).

Kernel Method (for Non-linear Separation)

In cases where the data are not linearly separable, SVM can still work by using the kernel method. This method allows transforming the data into a higher-dimensional space where they may become linearly separable.

Thus, SVM uses a kernel function that expresses the dot product between two points in the transformed space.

Common kernels include:

Linear kernel: $K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j$
Polynomial kernel: $K(\mathbf{x}_i, \mathbf{x}_j) = (\mathbf{x}_i \cdot \mathbf{x}_j + 1)^d$
Gaussian kernel (RBF): $K(\mathbf{x}_i, \mathbf{x}_j) = \exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2\sigma^2}\right)$

The kernel function allows SVM to work with non-linearly separable data, making the model much more flexible.

Code Example

In this example, we create a dataset with 8 points, each belonging to one of two classes. Four points belong to the first class (labeled as 1), and four points belong to the second class (labeled as -1). The points for Class 1 are clustered around the lower-left region of the feature space, while the points for Class -1 are clustered around the upper-right region. We use this dataset to train a Support Vector Machine (SVM) model with gradient descent.

The SVM model is initialized with a learning rate and regularization parameter, and is trained using the train method. The training involves iterating through the dataset and updating the weights and bias based on the gradient of the hinge loss. After training, the model's accuracy is evaluated on the same dataset.

To test the model, we use a new test point (5.0, 6.0) that lies near the decision boundary. The model's prediction for this new point is then displayed on the screen. This setup allows the SVM to learn a decision boundary that separates the two classes based on the feature space.

Dependencies

In the Cargo.toml file, add the dependency:

[dependencies]
rand = "0.8"

Code

use rand::Rng;

// Define a structure for the SVM model
#[derive(Debug)]
struct SVM {
    weights: Vec<f64>,  // Weights for the features
    bias: f64,          // Bias term (intercept)
    learning_rate: f64, // Learning rate for gradient descent
    regularization: f64, // Regularization parameter (C)
}

// Implement methods for the SVM model
impl SVM {
    // Constructor for the SVM struct
    fn new(num_features: usize, learning_rate: f64, regularization: f64) -> SVM {
        let mut rng = rand::thread_rng();
        SVM {
            weights: (0..num_features).map(|_| rng.gen_range(-0.1..0.1)).collect(),
            bias: 0.0,
            learning_rate,
            regularization,
        }
    }

    // Function to calculate the prediction for a single sample
    fn predict(&self, sample: &Vec<f64>) -> f64 {
        let dot_product: f64 = self.weights.iter().zip(sample.iter()).map(|(w, x)| w * x).sum();
        let decision_value = dot_product + self.bias;
        if decision_value >= 0.0 { 1.0 } else { -1.0 }
    }

    // Function to train the SVM using gradient descent
    fn train(&mut self, data: &Vec<Vec<f64>>, labels: &Vec<f64>, num_epochs: usize) {
        for _ in 0..num_epochs {
            for (i, sample) in data.iter().enumerate() {
                let label = labels[i];
                let dot_product: f64 = self.weights.iter().zip(sample.iter()).map(|(w, x)| w * x).sum();
                let decision_value = dot_product + self.bias;

                // Hinge loss gradient update
                if label * decision_value < 1.0 {
                    for j in 0..self.weights.len() {
                        self.weights[j] += self.learning_rate * (label * sample[j] - self.regularization * self.weights[j]);
                    }
                    self.bias += self.learning_rate * label;
                } else {
                    for j in 0..self.weights.len() {
                        self.weights[j] -= self.learning_rate * self.regularization * self.weights[j];
                    }
                }
            }
        }
    }

    // Function to evaluate the accuracy of the SVM model
    fn accuracy(&self, data: &Vec<Vec<f64>>, labels: &Vec<f64>) -> f64 {
        let correct_predictions = data.iter()
            .zip(labels.iter())
            .filter(|(sample, label)| self.predict(sample) == **label)
            .count();
        correct_predictions as f64 / data.len() as f64
    }
}

fn main() {
    // Example data (features and labels)
    let data = vec![
        vec![2.0, 3.0],  // Class 1
        vec![3.0, 2.0],  // Class 1
        vec![3.0, 3.0],  // Class 1
        vec![4.0, 2.0],  // Class 1
        vec![7.0, 7.0],  // Class -1
        vec![8.0, 8.0],  // Class -1
        vec![7.0, 9.0],  // Class -1
        vec![9.0, 8.0],  // Class -1
    ];

    let labels = vec![1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0]; // Target labels for each example

    // Create the SVM model
    let mut svm = SVM::new(2, 0.01, 0.01);  // 2 features, learning rate 0.01, regularization 0.01

    // Train the SVM model
    svm.train(&data, &labels, 1000);

    // Evaluate the accuracy of the model on the training data
    let accuracy = svm.accuracy(&data, &labels);
    println!("Model Accuracy: {:.2}%", accuracy * 100.0);

    // Make a prediction on a new example
    let new_sample = vec![5.0, 6.0];
    let prediction = svm.predict(&new_sample);
    println!("Prediction for new example: {}", prediction);
}

Output

Model Accuracy: 100.00%
Prediction for new example: -1

The model achieved 100% accuracy on the training data, correctly classifying all examples. However, the prediction for the new example indicates that it falls into the negative class.

Model Evaluation

After training and making predictions with an SVM model, it is important to evaluate its performance. Evaluation helps determine how well the model separates data into the correct classes and whether it is suitable for deployment in practice. For binary classification, we can use several classic metrics that help assess the quality of the model.

Accuracy

Accuracy is the most basic metric that shows the proportion of correct predictions out of the total number of predictions. It indicates what fraction of all predictions the model identified correctly.

$$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total number of predictions}}$$

If the dataset is imbalanced (e.g., 95% of class 0), accuracy can be misleading.

Accuracy of 90% or higher is generally considered good for balanced and noise-free datasets.

👉 A detailed explanation of Accuracy can be found in the section: Accuracy

Precision

Precision tells us how many of the predicted positive results were actually correct. It is important when avoiding false positives is critical (for example, in medicine where a wrong diagnosis can have serious consequences).

$$\text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}$$

Important when false positives are problematic (e.g., labeling a valid email as spam, or medicine diagnostics).

👉 A detailed explanation of Precision can be found in the section: Precision

Recall (Sensitivity)

Recall tells us how many of the actual positive cases the model correctly identified. It is important when minimizing false negatives is necessary, i.e., situations where the model misses real positive cases (for example, in cancer detection, where failing to detect a positive case can be dangerous).

$$\text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}$$

Important when false negatives are problematic (e.g., missing a disease diagnosis).

👉 A detailed explanation of Recall can be found in the section: Recall

F1 Score

The F1 score is the harmonic mean of precision and recall. It is very useful when both precision and recall need to be balanced. This metric is valuable when we want to consider both the correctness of positive predictions and the ability to find all actual positive cases.

$$\text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$

Especially useful for imbalanced class distributions.

F1 score of 0.8 or higher is generally considered good.

👉 A detailed explanation of F1 Score can be found in the section: F1 Score

Confusion Matrix

A confusion matrix is a table that summarizes the performance of a classification model by showing the counts of true positives, false positives, true negatives, and false negatives. It provides a detailed breakdown of how the model’s predictions compare to the actual labels and helps identify specific types of errors.

	Predicted Positive	Predicted Negative
Actual Positive	TP	FN
Actual Negative	FP	TN

TP (True Positives) – Correctly predicted positive cases.
TN (True Negatives) – Correctly predicted negative cases.
FP (False Positives) – Incorrectly predicted positive cases.
FN (False Negatives) – Incorrectly predicted negative cases.

Alternative Algorithms

There are several algorithms suitable for classification tasks. Each of these algorithms has its own advantages and disadvantages depending on the characteristics of the problem, data, and performance requirements.

Random Forest: Random Forest is an ensemble learning algorithm that creates multiple decision trees and combines their results to obtain a final prediction. This approach is very robust and effective for most tasks, including classification. Learn more
k-Nearest Neighbors (k-NN): K-Nearest Neighbors (k-NN) is easy to implement and effective for classification and regression. This algorithm does not use an explicit training process; instead, it makes predictions based on the nearest neighbors of a sample in the training dataset. Learn more
Logistic Regression: Logistic Regression is a linear model used for binary classification. It predicts the probability that a given point belongs to one of two classes. The model output is a probability, which is then transformed into a class based on a chosen threshold. Learn more
Naive Bayes: Naive Bayes is a classification algorithm based on Bayes' probability theory, which assumes that attributes are independent (this assumption is "naive," hence the name). Naive Bayes is very fast and efficient, especially for working with text or categorical data.
Neural Networks: Neural Networks are very powerful algorithms used for large and complex tasks. In classification, these models learn through multiple layers (so-called deep learning) and can model very complex and nonlinear patterns in data.

Advantages and Disadvantages

SVM is an excellent algorithm for problems involving nonlinear separations, high-dimensional data, and the need for strong generalization. On the other hand, its computational complexity and the need for careful hyperparameter tuning can be drawbacks, especially when working with large datasets or when fast real-time prediction is required. It is best suited for small to medium-sized problems where high accuracy is needed.

✅ Advantages:

High accuracy for nonlinear problems.
Ability to work with high-dimensional data.
Robustness against overfitting.

❌ Disadvantages:

Computationally intensive for large datasets.
Sensitive to the correct choice of kernel and hyperparameters.
Not very efficient for very large datasets or very fast predictions.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟢 Small / 🟡 Medium
Training Complexity	🔴 High

Use Case Examples

Image Classification

Used for categorizing images in various applications such as face recognition, object detection, or optical character recognition (OCR). For example, it can classify images into different categories like dog vs. cat.

Fraud Detection

Can be very effective in detecting fraudulent transactions because of its ability to uncover nonlinear patterns in data. In banking, SVM is used to identify unusual transactions that might indicate fraud.

Sentiment Analysis

Used for analyzing sentiment in textual data such as reviews, social media posts, or discussion forums. With SVM, texts can be classified into categories like positive or negative sentiment.

Medical Diagnosis

In medicine, SVM is applied to classify various health conditions based on different inputs such as medical images, genetic data, or clinical records. It can assist in diagnosing cancer, diabetes, or other diseases.

Conclusion

Support Vector Machines (SVM) is a machine learning algorithm particularly suitable for binary classification. Since its inception, this algorithm has established itself as an effective solution for various tasks that require separating data into two classes, especially in cases where the data is non-linearly separable. SVMs are used in many fields such as image recognition, spam detection, sentiment prediction, and medicine.

It can be somewhat challenging to properly tune and optimize the model’s parameters, but with appropriate settings, it can be a very powerful solution for classification problems. On the other hand, its computational complexity and sensitivity to hyperparameters need to be considered, as these can pose challenges for certain applications.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.