k-Nearest Neighbors

Machine Learning → Supervised Learning → Classification → Single Label Classification → Multi Class Classification

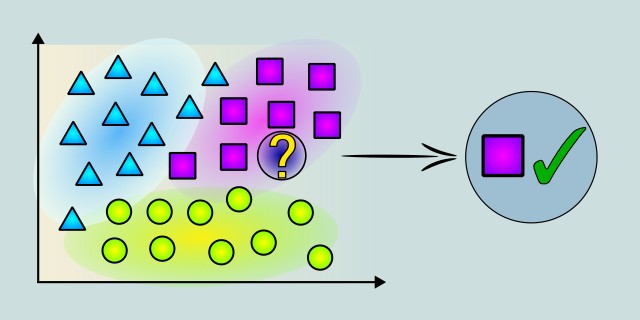
The k-Nearest Neighbors (k-NN) algorithm is one of the simplest methods used in supervised machine learning. Primarily applied to classification tasks, it can also be adapted for regression problems. As a lazy learning algorithm, k-NN does not construct a general internal model during training. Instead, it memorizes the training dataset and makes predictions only when new data needs to be classified. The k-NN algorithm is based on the idea that data points with similar features tend to be close to each other in the feature space. When a new data point needs to be classified, the algorithm looks for the 'k' closest points in the training set, using a distance metric like Euclidean distance to measure similarity. It then assigns the new point to the class that is most common among these nearest neighbors. Although k-NN may not always match the performance of more advanced models on large or complex datasets, its interpretability and ease of implementation make it an excellent choice for small-to medium-sized problems, especially when model transparency is important.

How It Works

The k-Nearest Neighbors (k-NN) algorithm works by comparing new data points to existing labeled data in order to make a prediction. Instead of learning a model during a training phase like many other algorithms, k-NN simply stores the training data and makes decisions at the moment of prediction. This approach is often referred to as lazy learning.

Imagine we have a small dataset of fruits with two features: weight and color. Each fruit is labeled as either an apple, banana, or orange. You receive a new, unlabeled fruit and want to determine what type it is.

The value of k (number of neighbors) is a critical parameter. A small k might be sensitive to noise, while a large k may smooth out distinctions between classes.

The distance metric (like Euclidean or Manhattan distance) affects how similarity is judged.

All features should be on a similar scale (e.g., normalized), or one feature may dominate the distance calculation.

Measure similarity

The algorithm calculates how similar the new fruit is to each fruit in the training set. This similarity is usually measured using distance in the feature space (commonly Euclidean distance).

Find the k nearest neighbors

Once all distances are calculated, the algorithm selects the k fruits that are closest to the new one. These are the neighbors that will be considered for voting.

Vote on the labe

Among the k nearest neighbors, the algorithm checks how many are apples, how many are bananas, and how many are oranges. The most common class among them is assigned as the label for the new fruit.

For instance, if k = 5 and among the 5 nearest fruits, 3 are apples, 1 is a banana, and 1 is an orange, then the new fruit will be classified as an apple.

Mathematical Foundation

While the k-Nearest Neighbors algorithm is conceptually simple, it relies on a few important mathematical principles. Understanding these can help clarify how predictions are made and how to tune the algorithm effectively.

Distance Metric

At the heart of k-NN is the idea of distance between data points. The most commonly used metric is the Euclidean distance, which measures the straight-line distance between two points in multidimensional space.

For two points $x = (x_1, x_2, ..., x_n)$ and $y = (y_1, y_2, ..., y_n)$, the Euclidean distance $d(x, y)$ is:

$$d(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2}$$

Other commonly used distance metrics include:

Manhattan Distance: Measures the distance between two points by summing the absolute differences of their coordinates.

$$d(x, y) = |x_1 - y_1| + |x_2 - y_2| + \cdots + |x_n - y_n|$$

Minkowski distance: The Minkowski distance is a generalization of both the Euclidean and Manhattan distances.

$$dd(x, y) = \left( \sum_{i=1}^n |x_i - y_i|^p \right)^{1/p}$$

$p = 2$ is the Euclidean distance.
$p = 1$ is the Manhattan distance.

Choose a distance metric that aligns with the structure of your data. Euclidean works well when features are continuous and equally scaled.

Voting Mechanism

After computing the distances between the test point and all points in the training set, the algorithm selects the $k$ nearest points. For classification tasks, it applies majority voting:

$$\hat{y} = \text{mode}(\{ y_{(1)}, y_{(2)}, ..., y_{(k)} \})$$

$y_{(i)}$ is the class label of the $i^{th}$ nearest neighbor.
$\hat{y}$ is the predicted class label.

For regression tasks (less common), the algorithm usually takes the average of the target values of the neighbors:

$$\hat{y} = \frac{1}{k} \sum_{i=1}^k y_{(i)}$$

Feature Scaling

Because k-NN relies heavily on distance calculations, all features should contribute equally to the distance. This requires normalization or standardization of features.

Min-max normalization:

$$x' = \frac{x - \min(x)}{\max(x) - \min(x)}$$

Z-score standardization:

$$x' = \frac{x - \mu}{\sigma}$$

Always scale your data before applying k-NN unless you're sure all features are already on a comparable scale.

Choosing k

The value of $k$ significantly influences performance. A small $k$ (e.g., 1) can lead to overfitting and sensitivity to noise. A large $k$ smooths predictions but may cause underfitting by ignoring local structure.

Start with odd values of $k$ (like 3, 5, 7) to reduce the chance of ties in binary classification.

Code Example

Dependencies

Add to your Cargo.toml:

[dependencies]
ndarray = "0.15.4"

Code

The process begins by manually defining a small dataset of 2D points, each labeled with a class ("A" or "B"). We then define a k-NN classifier with $k = 3$, meaning the algorithm will consider the three nearest neighbors when making a prediction. Instead of using a separate training and test set, we apply the classifier directly to a single query point to determine its class based on the existing labeled data. The prediction is made using majority voting among the nearest neighbors. Finally, the result is printed to the console, showing the predicted class of the query point.

use ndarray::Array1;
use std::cmp::Ordering;

#[derive(Debug)]
struct DataPoint {
    features: Array1<f64>,
    label: String,
}

fn euclidean_distance(a: &Array1<f64>, b: &Array1<f64>) -> f64 {
    a.iter()
        .zip(b.iter())
        .map(|(x, y)| (x - y).powi(2))
        .sum::<f64>()
        .sqrt()
}

fn knn_classify(data: &[DataPoint], query: &Array1<f64>, k: usize) -> String {
    let mut distances: Vec<(f64, &str)> = data
        .iter()
        .map(|point| (euclidean_distance(&point.features, query), point.label.as_str()))
        .collect();

    // Sort by distance
    distances.sort_by(|a, b| a.0.partial_cmp(&b.0).unwrap_or(Ordering::Equal));

    // Count the top-k labels
    let mut label_count = std::collections::HashMap::new();
    for &(_, label) in distances.iter().take(k) {
        *label_count.entry(label).or_insert(0) += 1;
    }

    // Return the label with the highest count
    label_count
        .into_iter()
        .max_by_key(|&(_, count)| count)
        .map(|(label, _)| label.to_string())
        .unwrap_or_else(|| "Unknown".to_string())
}

fn main() {
    // Example dataset
    let data = vec![
        DataPoint {
            features: Array1::from_vec(vec![1.0, 2.0]),
            label: "A".to_string(),
        },
        DataPoint {
            features: Array1::from_vec(vec![2.0, 3.0]),
            label: "A".to_string(),
        },
        DataPoint {
            features: Array1::from_vec(vec![3.0, 3.0]),
            label: "B".to_string(),
        },
        DataPoint {
            features: Array1::from_vec(vec![6.0, 7.0]),
            label: "B".to_string(),
        },
    ];

    // Query point
    let query = Array1::from_vec(vec![2.5, 3.0]);

    let k = 3;
    let predicted = knn_classify(&data, &query, k);

    println!("Predicted class: {}", predicted);
}

Output

Predicted class: A

The output will be the **predicted label** of the query point, based on the most common label among its 3 nearest neighbors.

Model Evaluation

In the case of k-Nearest Neighbors (k-NN) for classification, several standard metrics are used to assess model quality. Each provides insight into different aspects of the model's behavior.

Accuracy

Accuracy is the most basic metric that shows the proportion of correct predictions out of the total number of predictions. It indicates what fraction of all predictions the model identified correctly.

$$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total number of predictions}}$$

If the dataset is imbalanced (e.g., 95% of class 0), accuracy can be misleading.

Accuracy of 90% or higher is generally considered good for balanced and noise-free datasets.

👉 A detailed explanation of Accuracy can be found in the section: Accuracy

Precision

Precision tells us how many of the predicted positive results were actually correct. It is important when avoiding false positives is critical (for example, in medicine where a wrong diagnosis can have serious consequences).

$$\text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}$$

Important when false positives are problematic (e.g., labeling a valid email as spam, or medicine diagnostics).

👉 A detailed explanation of Precision can be found in the section: Precision

Recall (Sensitivity)

Recall tells us how many of the actual positive cases the model correctly identified. It is important when minimizing false negatives is necessary, i.e., situations where the model misses real positive cases (for example, in cancer detection, where failing to detect a positive case can be dangerous).

$$\text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}$$

Important when false negatives are problematic (e.g., missing a disease diagnosis).

👉 A detailed explanation of Recall can be found in the section: Recall

F1 Score

The F1 score is the harmonic mean of precision and recall. It is very useful when both precision and recall need to be balanced. This metric is valuable when we want to consider both the correctness of positive predictions and the ability to find all actual positive cases.

$$\text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$

Especially useful for imbalanced class distributions.

F1 score of 0.8 or higher is generally considered good.

👉 A detailed explanation of F1 Score can be found in the section: F1 Score

Confusion Matrix

A confusion matrix is a table that summarizes the performance of a classification model by showing the counts of true positives, false positives, true negatives, and false negatives. It provides a detailed breakdown of how the model’s predictions compare to the actual labels and helps identify specific types of errors.

	Predicted Positive	Predicted Negative
Actual Positive	TP	FN
Actual Negative	FP	TN

TP (True Positives) – Correctly predicted positive cases.
TN (True Negatives) – Correctly predicted negative cases.
FP (False Positives) – Incorrectly predicted positive cases.
FN (False Negatives) – Incorrectly predicted negative cases.

Cross-Validation Accuracy

Cross-validation accuracy measures how well a model performs on unseen data by repeatedly splitting the dataset into training and testing parts. For example, in k-fold cross-validation, the data is divided into k parts, and the model is trained k times, each time leaving out a different part for testing. This helps obtain a more reliable estimate of model performance than a single train-test split.

Low variability in performance across cross-validation folds suggests that the model is stable and generalizes well.

Alternative Algorithms

While k-Nearest Neighbors (k-NN) is a straightforward and intuitive algorithm for classification and regression tasks, there are many alternative algorithms that can be used depending on the dataset, problem complexity, and performance requirements.

Decision Trees: Unlike k-NN, decision trees create an explicit model, making them more interpretable. Suitable for both classification and regression; works well with categorical features and when interpretability is important. Learn more
Random Forest: Ensemble of decision trees that improve accuracy by averaging multiple trees. More accurate and robust than k-NN; handles large feature sets well. Learn more
Support Vector Machines (SVM): SVMs can handle high-dimensional data better than k-NN and are more robust to noise. Effective for complex but small-to-medium sized datasets; good for binary classification. Learn more
Logistic Regression: Statistical model predicting probability of a binary outcome. Unlike k-NN’s instance-based approach, logistic regression learns coefficients for features. Learn more
Naive Bayes: Probabilistic classifier based on Bayes’ theorem assuming feature independence. Faster than k-NN for large datasets; good baseline for text classification.

Advantages and Disadvantages

k-NN’s simplicity and flexibility make it a powerful tool for many problems, but its computational cost, sensitivity to data quality, and challenges in high dimensions limit its effectiveness in some scenarios. Proper data preprocessing and hyperparameter tuning are essential for good performance.

✅ Advantages:

k-NN is straightforward to understand and implement, making it a great starting point for classification and regression problems.
k-NN does not require an explicit training phase. It simply stores the training data and performs computation during prediction, which makes it easy to update with new data.
k-NN can be applied to both classification and regression tasks without modification.
k-NN makes no assumptions about the underlying data distribution, allowing it to model complex relationships naturally.
k-NN handles multi-class classification tasks well, as predictions depend on the nearest neighbors’ labels.

❌ Disadvantages:

Since k-NN compares the new data point to all training samples, prediction can be slow and resource-intensive, especially with large datasets.
The algorithm relies heavily on distance calculations, so irrelevant or noisy features can degrade performance unless proper feature selection or scaling is applied.
Selecting an inappropriate number of neighbors can lead to overfitting (small k) or underfitting (large k). Finding the optimal k requires experimentation.
In high-dimensional spaces, distance metrics become less meaningful, and k-NN’s performance often deteriorates unless dimensionality reduction is applied.
Because k-NN is an instance-based learner, it does not provide a generalizable model or explicit decision boundary, making interpretation difficult.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium
Training Complexity	🟢 Low

Use Case Examples

Handwritten Digit Recognition (e.g., MNIST)

In optical character recognition (OCR) systems, k-NN is used to classify handwritten digits. Each digit image is converted into a vector of pixel values, and the algorithm finds the most similar digits from the training set to determine the correct label.

Recommender Systems

In content-based recommendation systems (e.g., movies, books, or music), k-NN helps suggest items similar to what a user has already liked by finding items with similar attributes or user ratings.

Medical Diagnosis

k-NN is used to classify medical conditions based on symptoms or test results. For example, in diagnosing diabetes or heart disease, the algorithm compares a patient's features to past cases.

Credit Risk Assessment

Banks and financial institutions use k-NN to evaluate whether loan applicants are likely to default, based on attributes like income, age, employment, and past credit behavior.

Anomaly Detection in Sensor Networks

k-NN can be used to detect abnormal readings from sensors in industrial systems, smart homes, or environmental monitoring setups.

Conclusion

k-NN requires no explicit training phase, making it ideal for scenarios where the dataset changes frequently or when quick experimentation is needed. It handles multi-class problems naturally, works well with small to medium datasets, and requires minimal assumptions about the data. Its core principle is to predict outcomes by comparing new data points to the most similar known examples. This approach reflects the intuitive way people often make decisions by relating unfamiliar situations to past experiences.

However, its effectiveness depends on careful data preparation. Since it relies on distance calculations, it is sensitive to irrelevant features, noise, and differing feature scales. Moreover, k-NN can become computationally expensive as the size of the dataset increases, and it may struggle with high-dimensional data unless dimensionality is reduced.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.