K-Means

Machine Learning → Unsupervised Learning → Clustering

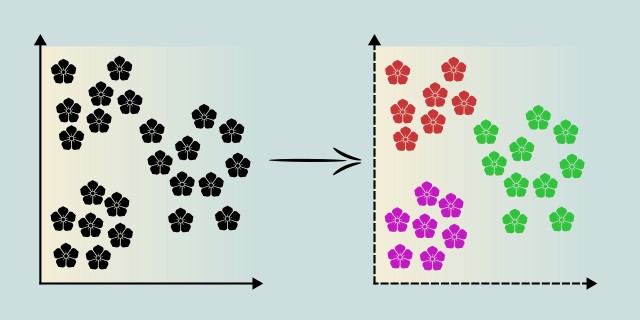
K-Means Clustering is a fundamental unsupervised learning algorithm widely used in data analysis and pattern recognition. This algorithm helps us discover hidden patterns or groupings within unlabelled data, making it invaluable for various applications such as market segmentation, image compression, and anomaly detection. It is used for various applications such as market segmentation, image compression, and anomaly detection.

At its core, K-Means Clustering is a method to partition a dataset into 'k' distinct clusters, where each cluster is represented by its center point, called a centroid. The algorithm iteratively assigns data points to the nearest centroid and then recalculates the centroids based on the mean position of all points assigned to each cluster.

How It Works

K-Means Clustering is an iterative algorithm that partitions a dataset into 'k' distinct clusters. The process involves several straightforward steps, which are repeated until the clusters stabilize.

Let’s say we’re analyzing mall customer data (age and spending), and we want to segment them into 3 distinct groups; such as young low spenders, middle-aged high spenders, and older budget-conscious shoppers.

Initialization

We begin by selecting 'k' initial centroids. These centroids are typically chosen randomly from the dataset. The choice of initial centroids can significantly impact the final clusters, so we often perform multiple runs with different initializations to ensure robustness.

For instance, we might randomly pick three customers: one young and thrifty, one middle-aged and high-spending, and one older with low spending. These serve as our starting centroids.

Assignment Step

Next, we assign each data point to the nearest centroid. The distance between a data point and a centroid is usually measured using the Euclidean distance, although other distance metrics can be applied depending on the context. This step forms 'k' clusters, where each cluster consists of all data points assigned to a particular centroid.

Each customer is now grouped with the centroid that best matches their profile. So similar customers naturally fall into the same cluster based on age and spending.

Update Step

We then recalculate the centroids of the clusters. The new centroid for each cluster is the mean (average) of all the data points assigned to it. This step updates the centroid positions to better reflect the center of each cluster.

If one cluster contains customers aged 22, 24, and 25 with monthly spending of 190–220, we compute their average age and spending to update the cluster's centroid.

Iteration

We repeat the assignment and update steps until the centroids no longer change significantly or until we reach a predefined number of iterations. Convergence is typically determined by checking whether the centroids move less than a specified threshold between steps.

After a few iterations, the clusters stabilize. Young low spenders stay grouped together, middle-aged high spenders in another group, and older budget shoppers in a third.

Termination

The algorithm terminates once the centroids stabilize, meaning that further reassignments do not significantly change the cluster centers. At this point, the final clusters are formed, and each data point belongs to the cluster whose centroid it is closest to.

We now have three well-defined customer segments that can guide decisions, such as tailored marketing strategies or personalized offers.

Notes

Choice of 'k': The number of clusters 'k' must be chosen beforehand. Selecting the right 'k' is essential and can be informed by methods like the Elbow Method or Silhouette Analysis.

If we had chosen k = 2 or k = 4, the resulting segments would look different. Either combining or further dividing existing groups.

Distance Metric: While Euclidean distance is commonly used, other distance metrics can be more suitable depending on the data characteristics.

For datasets involving non-numerical features or weighted attributes, we might opt for Manhattan or cosine distance instead.

Random Initialization: Since the initial centroids are chosen randomly, different runs may yield different results. Running the algorithm multiple times and selecting the best outcome helps improve consistency.

We often run the algorithm several times and choose the solution with the lowest overall clustering error (inertia).

Mathematical Foundation

The K-Means Clustering algorithm relies on several core mathematical concepts to partition a dataset into $k$ clusters by minimizing intra-cluster variance.

Objective Function

The goal of K-Means is to minimize the total sum of squared distances between each data point and the centroid of its assigned cluster.

This is formalized by the following objective function:

$$J = \sum_{i=1}^{k} \sum_{x \in C_i} \|x - \mu_i\|^2$$

$J$ is the total within-cluster sum of squares (WCSS), the function K-Means aims to minimize.
$k$ is the number of clusters.
$C_i$ is the set of data points assigned to cluster $ i $.
$x$ is an individual data point.
$\mu_i$ is the centroid of cluster $ i $.
$\|x - \mu_i\|^2$ is the Euclidean distance between point $x$ and centroid $\mu_i$.

Minimizing $J$ means we're trying to make each cluster as tight as possible around its centroid.

Euclidean Distance

K-Means typically uses Euclidean distance to measure similarity. For a point $x \in \mathbb{R}^d$ and a centroid $\mu_i \in \mathbb{R}^d$, the distance is calculated as:

$$\|x - \mu_i\| = \sqrt{\sum_{j=1}^{d} (x_j - \mu_{ij})^2}$$

$d$ is the number of dimensions (features) in the dataset.
$x_j$ and $\mu_{ij}$ are the $j$-th components of $x$ and $\mu_i$, respectively.

This formula computes the straight-line distance in multi-dimensional space.

Centroid Calculation

The centroid of a cluster is the mean of all data points assigned to that cluster. It is recalculated in each iteration:

$$\mu_i = \frac{1}{|C_i|} \sum_{x \in C_i} x$$

$|C_i|$ is the number of points in cluster $ i $.

This step “pulls” the centroid toward the center of its current members.

Algorithm Steps

Initialization: Randomly select $k$ initial centroids:
$$\mu_1, \mu_2, \ldots, \mu_k$$
Assignment Step: Assign each point $x$ to the cluster with the nearest centroid:
$$C_i = \left\{x \mid \|x - \mu_i\| \leq \|x - \mu_j\| \quad \forall j \neq i \right\}$$
Update Step: Recompute each centroid as the mean of the points in its cluster:
$$\mu_i = \frac{1}{|C_i|} \sum_{x \in C_i} x$$
Iteration: Repeat steps 2 and 3 until convergence.
Each iteration reduces the value of the objective function $J$.

Convergence Criteria

K-Means is considered to have converged when the change in the objective function $J$ falls below a threshold $\epsilon$:

$$|J_{\text{new}} - J_{\text{old}}| < \epsilon$$

Alternatively, we may terminate the algorithm after a fixed number of iterations if convergence is slow or to reduce computation.

Notes

Choice of 'k': The number of clusters must be predefined. Techniques such as the Elbow Method, Silhouette Score, or Gap Statistic can help estimate the optimal value of $k$.

In a customer segmentation task, trying different values of $k$ can help us discover the natural number of customer groups (e.g., 3–5 segments).

Distance Metric: While Euclidean distance is the default, others like Manhattan or Cosine distance may be more appropriate depending on data type and distribution.

If our customer data includes categorical features or varied scales, we may need to switch metrics or normalize the data first.

Random Initialization: Because centroids are initially selected at random, K-Means can converge to different local minima.

To reduce this sensitivity, we can run the algorithm multiple times or use the smarter K-Means++ initialization, which chooses initial centroids more strategically.

Code Example

In this example, we'll implement a simple version of the K-Means Clustering algorithm in Rust using a dataset of customers described by two features: age and monthly spending.

Dependencies

Add to your Cargo.toml:

[dependencies]
ndarray = "0.15"
rand = "0.8"

Code

use ndarray::{Array2, Array1, Axis, array};
use rand::seq::SliceRandom;
use rand::thread_rng;

const K: usize = 3; // Number of clusters
const MAX_ITER: usize = 100;
const TOLERANCE: f64 = 1e-4;

fn euclidean_distance(a: &Array1<f64>, b: &Array1<f64>) -> f64 {
    a.iter().zip(b.iter())
     .map(|(x, y)| (x - y).powi(2))
     .sum::<f64>()
     .sqrt()
}

fn main() {
    // 1. Define dataset (9 customers, 2 features: age and spending)
    let data = array![
        [22.0, 200.0],
        [25.0, 220.0],
        [24.0, 190.0],
        [35.0, 400.0],
        [40.0, 380.0],
        [38.0, 420.0],
        [55.0, 100.0],
        [58.0, 130.0],
        [53.0, 90.0],
    ];

    let mut rng = thread_rng();
    let n_samples = data.nrows();
    let n_features = data.ncols();

    // 2. Initialize centroids by randomly selecting K data points
    let mut indices: Vec<_> = (0..n_samples).collect();
    indices.shuffle(&mut rng);
    let mut centroids = data.select(Axis(0), &indices[..K]);

    let mut labels = vec![0; n_samples];

    for _ in 0..MAX_ITER {
        let mut new_labels = vec![0; n_samples];

        // 3. Assignment Step: Assign each point to the nearest centroid
        for (i, point) in data.outer_iter().enumerate() {
            let (label, _) = centroids.outer_iter()
                .enumerate()
                .map(|(j, centroid)| (j, euclidean_distance(&point.to_owned(), &centroid.to_owned())))
                .min_by(|a, b| a.1.partial_cmp(&b.1).unwrap())
                .unwrap();
            new_labels[i] = label;
        }

        // 4. Update Step: Recalculate centroids
        let mut new_centroids = Array2::<f64>::zeros((K, n_features));
        let mut counts = vec![0; K];

        for (i, label) in new_labels.iter().enumerate() {
            let point = data.row(i);
            new_centroids
                .row_mut(*label)
                .iter_mut()
                .zip(point.iter())
                .for_each(|(c, &v)| *c += v);
            counts[*label] += 1;
        }

        for (i, count) in counts.iter().enumerate() {
            if *count > 0 {
                new_centroids
                    .row_mut(i)
                    .iter_mut()
                    .for_each(|v| *v /= *count as f64);
            }
        }

        // 5. Check for convergence
        let shift: f64 = centroids
            .outer_iter()
            .zip(new_centroids.outer_iter())
            .map(|(a, b)| euclidean_distance(&a.to_owned(), &b.to_owned()))
            .sum();

        if shift < TOLERANCE {
            break;
        }

        centroids = new_centroids;
        labels = new_labels;
    }

    // Output results
    println!("Final centroids:\n{}", centroids);
    println!("Cluster assignments: {:?}", labels);
}

We start by randomly initializing three centroids from the data set. Then, we assign each customer (represented by age and monthly spending) to the nearest centroid using Euclidean distance. After assigning all points, the algorithm recalculates the centroids by calculating the average of all points within each cluster. The assignment and update are repeated iteratively until the centroids stabilize, meaning that they no longer change significantly between iterations. Finally, the program prints the resulting centroids and cluster assignments for each customer, dividing them into three distinct groups based on their characteristics.

Output

Final centroids:
[[37.666666666666664, 400],
 [23.666666666666668, 203.33333333333334],
 [55.333333333333336, 106.66666666666667]]
Cluster assignments: [1, 1, 1, 0, 0, 0, 2, 2, 2]

Cluster 0: Young, lower-spending customers.
Cluster 1: Middle-aged, high-spending customers.
Cluster 2: Older, budget-conscious customers.

Model Evaluation

Evaluating the performance of a K-Means clustering model is more nuanced than with supervised learning because there are no predefined labels. Instead, we use internal and external metrics (when ground truth is available) to assess how well the data has been partitioned into clusters.

Inertia (Within-Cluster Sum of Squares)

Inertia is the sum of squared distances between each data point and the centroid of its assigned cluster. This is the same objective function that K-Means tries to minimize:

$$\text{Inertia} = \sum_{i=1}^{k} \sum_{x \in C_i} \|x - \mu_i\|^2$$

After clustering customers, a low inertia means customers in each group behave similarly (e.g., similar age and spending).

Elbow Method

The Elbow Method helps determine the optimal number of clusters $k$. We compute the inertia for different values of $k$, then plot them to find the "elbow" point where the inertia starts to decrease more slowly:

Plot $k$ on the x-axis and inertia on the y-axis.
The "elbow" indicates a good trade-off between compactness and complexity.

For example, if the elbow appears at $k = 3$, it likely reflects three distinct customer segments.

Silhouette Score (Internal)

Evaluates how similar each point is to its own cluster vs. others, after “cutting” the dendrogram into flat clusters. It ranges from -1 to 1:

$$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$$

$a(i)$: mean intra-cluster distance (how close point $i$ is to others in its own cluster).
$b(i)$: mean nearest-cluster distance (how close point $i$ is to points in the nearest different).

A score close to 1 means the point is well matched to its cluster.
A score near 0 means the point lies between two clusters.
A negative score indicates potential misclassification.

After segmenting customers, a high average silhouette score means most customers clearly belong to one group.

Davies–Bouldin Index

The Davies–Bouldin Index measures intra-cluster similarity and inter-cluster difference. Lower values are better:

It compares the distance between cluster centroids to the size (spread) of the clusters.
A score close to 0 indicates well-separated, tight clusters.

Adjusted Rand Index (External)

If ground truth labels are available (e.g., known customer types), the Adjusted Rand Index can compare the predicted clusters to the true labels.

ARI ranges from -1 (poor agreement) to 1 (perfect match).
Values near 0 suggest random labeling.

Alternative Algorithms

Hierarchical Clustering: Builds a tree (dendrogram) of clusters by either merging or splitting them step by step. Better than K-Means when we want a nested structure (e.g., categorizing customers into broader and narrower segments). Learn more
DBSCAN: Groups together points that are closely packed and marks outliers as noise. Ideal when we expect noisy data or clusters with unusual shapes, such as in geospatial or sensor data. Learn more
Mean Shift: A centroid-based algorithm like K-Means but without the need to predefine the number of clusters. Useful when we want automatic cluster discovery and can afford higher computational cost.
Gaussian Mixture Models (GMM): A probabilistic model that assumes data is generated from a mixture of several Gaussian distributions. Better suited than K-Means when clusters are overlapping or have elliptical shapes (e.g., financial data).
Spectral Clustering Uses the spectrum (eigenvalues) of a similarity matrix to reduce dimensionality before clustering. Effective when the dataset structure is non-convex or best represented as a graph (e.g., social networks).

Advantages and Disadvantages

While K-Means Clustering is one of the most popular unsupervised learning algorithms due to its efficiency and simplicity, it has several limitations that make it unsuitable for certain types of data or tasks.

✅ Advantages:

K-Means is easy to implement and computationally efficient, especially on large datasets with few features.
It scales well to large datasets and is often used as a baseline clustering algorithm.
The resulting clusters and centroids are intuitive and easy to understand, especially for low-dimensional data.
K-Means is widely used across domains: marketing, image compression, customer segmentation, document clustering, and more.
It performs well when clusters are compact, clearly separated, and of similar size and density.

For example, when segmenting customers into young/low-spend, middle/high-spend, and older/low-spend groups, K-Means can often detect clear patterns.

❌ Disadvantages:

The number of clusters must be chosen beforehand, and selecting the "right" $k$ is not always straightforward.
K-Means tends to perform poorly when clusters are non-spherical, elongated, or have unequal sizes.
Randomly chosen initial centroids can lead to suboptimal solutions. Multiple runs or K-Means++ can help mitigate this.
A single outlier can significantly skew the centroid, affecting cluster quality.
K-Means is not suitable for data with overlapping clusters, varying density, or manifold structure.

If customer behaviors follow overlapping or irregular patterns, K-Means may wrongly assign individuals to the wrong group.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium / 🔴 Large
Training Complexity	🟡 Medium

Use Case Examples

Customer Segmentation (Marketing)

Businesses often use K-Means to group customers based on purchasing behavior, demographics, or engagement metrics. Enables targeted marketing campaigns or personalized product recommendations.

Image Compression

K-Means can reduce the number of colors in an image while preserving visual quality. Each pixel is replaced with the nearest cluster centroid (representing a dominant color), reducing color depth from thousands to just a few dozen.

Document Clustering

Text documents can be clustered into thematic groups based on word usage patterns. Automates categorization and improves content discovery. News articles might be grouped into categories like sports, politics, and technology based on word frequencies.

Anomaly Detection in Sensor Data

K-Means can identify normal patterns in data and flag deviations as potential anomalies. Increases reliability and safety in monitored systems. An equipment monitoring system may detect a cluster of abnormal readings outside the usual operating range.

Geographical Data Analysis

K-Means helps cluster locations or coordinates in spatial datasets. Supports location-based decision-making. A delivery company might cluster delivery addresses to optimize route planning by grouping nearby destinations.

Conclusion

K-Means is a fast, intuitive, and widely used clustering algorithm that excels in situations where we want to uncover structure in unlabeled data. It partitions data into distinct, non-overlapping clusters based on similarity. However, its performance depends heavily on the correct choice of the number of clusters $k$, the scale and distribution of the data, and the initial placement of centroids. When applied appropriately, K-Means can provide powerful insights into structure and patterns in data that might otherwise go unnoticed.

K-Means works best when the number of clusters is known or can be reasonably estimated, and when clusters are well-separated, spherical, and roughly equal in size and density. However, it may not be the best choice when the data contains significant noise or outliers, when clusters have irregular shapes or widely varying densities, or when there is a need to determine the number of clusters automatically. In such cases, alternative clustering algorithms like DBSCAN, Gaussian Mixture Models, or hierarchical clustering may offer more robust or flexible results.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.