Hierarchical Clustering

Machine Learning → Unsupervised Learning → Clustering

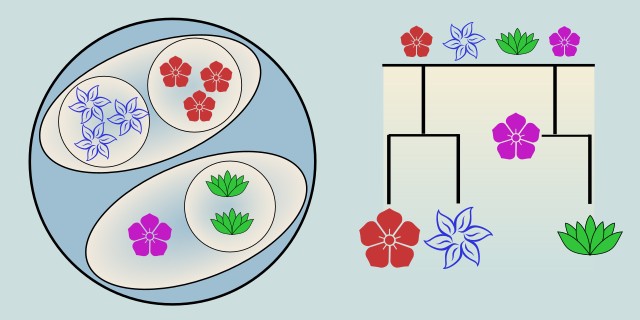
Hierarchical Clustering is an unsupervised machine learning algorithm that builds a hierarchy of clusters using a bottom-up (agglomerative) or top-down (divisive) approach. Unlike methods that group data into a fixed number of clusters, hierarchical clustering produces a tree-like structure (called a dendrogram) that shows how clusters are formed step by step.

This algorithm is commonly used in domains like biology (e.g., gene expression analysis), text mining, customer segmentation, and image classification.

How It Works

Hierarchical Clustering works by building a tree of clusters. This tree shows how individual data points are grouped step by step based on their similarity (or distance). There are two main types Agglomerative (bottom-up) and Divisive (top-down).

We'll focus on agglomerative clustering, as it's more widely used.

Example

Let's imagine that we run a small library. We want to organize books according to how similar they are. For example, by genre, writing style, length, and complexity. We don't know how many categories we will end up with, so we decide to use hierarchical clustering.

1. Start with each item as its own cluster

Each book is its own individual cluster. So if you have 10 books, you start with 10 separate clusters.

2. Calculate the distance (or similarity) between all clusters

You compute how similar each book is to every other book using a distance metric (like Euclidean or cosine similarity). Let’s say Book A and Book B are the most similar pair, they both are fantasy novels, 300 pages long, and written in a similar tone.

3. Merge the closest pair of clusters

You merge Book A and Book B into one cluster. Now you have 9 clusters.

4. Recalculate distances

Next, you calculate the distance between this new cluster (A+B) and every other remaining cluster. This step depends on the linkage method you choose:

Single linkage: use the closest distance between two points in the clusters.
Complete linkage: use the farthest distance between two points.
Average linkage: use the average distance between all points.
Ward's method: minimizes the increase in total variance.

Each linkage strategy affects how the final tree structure forms.

5. Repeat

Keep merging the two closest clusters and updating the distances each time. This process continues until all items are merged into a single cluster, or until we choose a cut-off point in the dendrogram to stop and define the clusters.

The Dendrogram

The result is a dendrogram, a tree diagram that shows the sequence of cluster merges. The height of each branch shows the distance (or dissimilarity) between clusters when they were merged.

By “cutting” the tree at a certain height (threshold), you define how many final clusters you want.

Mathematical Foundation

Hierarchical clustering is built around distance measurements and linkage methods. The algorithm repeatedly merges the two clusters that are closest together according to a chosen metric.

Distance Between Data Points

We calculate the distances between all points and create a distance matrix. To begin clustering, we need a way to measure how similar or different data points are.

Euclidean Distance (most used):

$$d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + \ldots + (p_n - q_n)^2}$$

Manhattan Distance:

$$d(p, q) = \sum_{i=1}^{n} |p_i - q_i|$$

Cosine Distance(especially for text or high-dimensional data):

$$\text{cosine\_distance}(p, q) = 1 - \frac{p \cdot q}{\|p\| \cdot \|q\|}$$

Distance Between Clusters (Linkage Criteria)

As we merge clusters, we need a way to define the distance between two clusters, not just two points. This is where linkage methods come in.

Let $A$ and $B$ be two clusters.

Single Linkage (Minimum Linkage):

Looks for the closest pair of points across clusters. Can result in long, chain-like clusters (can be sensitive to noise).

$$D(A, B) = \min_{a \in A, b \in B} d(a, b)$$

Complete Linkage (Maximum Linkage):

Considers the farthest points, leads to compact and tight clusters.

$$D(A, B) = \max_{a \in A, b \in B} d(a, b)$$

Average Linkage:

Averages all pairwise distances between the two clusters.

$$D(A, B) = \frac{1}{|A||B|} \sum_{a \in A} \sum_{b \in B} d(a, b)$$

A good balance between single and complete linkage.

Ward’s Method(Minimum Variance):

Ward’s method merges the pair of clusters that results in the smallest increase in total within-cluster variance.

The idea is to minimize:

$$\Delta E = \sum_{i=1}^{k} \sum_{x \in C_i} \|x - \mu_i\|^2$$

$C_i$ is the cluster.
$\mu_i$ is the centroid (mean) of cluster $C_i$.

Ward’s method generally results in compact, well-separated clusters.

Dendrogram and Cluster Selection

Once all points are merged into a single cluster, we can build a dendrogram, a visual tree showing how clusters were joined at each step.

To decide how many clusters to keep, we can visually “cut” the dendrogram at a chosen height or set a threshold distance (e.g., don’t merge clusters whose distance is > τ).

Code Example

We’ll simulate a basic agglomerative clustering approach using pairwise distances and walk through the concept manually, suitable for small datasets. Define a simple 2D data set and calculate the pairwise distance matrix using Euclidean distance.

Dependencies

To run this code, make sure you add the following dependencies in your Cargo.toml:

[dependencies]
ndarray = "0.15"

Code

use ndarray::Array2;
use std::f64;

fn euclidean_distance(p1: &[f64], p2: &[f64]) -> f64 {
    p1.iter()
        .zip(p2.iter())
        .map(|(a, b)| (a - b).powi(2))
        .sum::<f64>()
        .sqrt()
}

fn main() {
    // Step 1: Define a simple dataset (each row is a 2D point)
    let data = vec![
        vec![1.0, 2.0],
        vec![1.5, 1.8],
        vec![5.0, 8.0],
        vec![8.0, 8.0],
    ];

    let n = data.len();

    // Step 2: Compute the pairwise distance matrix
    let mut dist_matrix = Array2::<f64>::zeros((n, n));

    for i in 0..n {
        for j in 0..n {
            if i != j {
                dist_matrix[[i, j]] = euclidean_distance(&data[i], &data[j]);
            } else {
                dist_matrix[[i, j]] = f64::INFINITY; // We ignore self-distances
            }
        }
    }

    // Step 3: Print the distance matrix
    println!("Pairwise distance matrix:");
    for row in dist_matrix.rows() {
        for val in row.iter() {
            print!("{:.2} ", val);
        }
        println!();
    }

    // Step 4: Find the closest pair (for demonstration, one merge step)
    let mut min_dist = f64::INFINITY;
    let mut pair = (0, 0);

    for i in 0..n {
        for j in 0..n {
            if dist_matrix[[i, j]] < min_dist {
                min_dist = dist_matrix[[i, j]];
                pair = (i, j);
            }
        }
    }

    println!(
        "\nClosest pair to merge first (single-linkage): Point {} and Point {} (distance = {:.2})",
        pair.0, pair.1, min_dist
    );

    // Further steps would involve:
    // - Merging these two points into a cluster
    // - Updating the distance matrix with the new cluster
    // - Repeating until only one cluster remains
}

Output

Pairwise distance matrix:
inf 0.54 7.21 9.22 
0.54 inf 7.12 8.98
7.21 7.12 inf 3.00
9.22 8.98 3.00 inf

Closest pair to merge first (single-linkage): Point 0 and Point 1 (distance = 0.54)

Normally, we would merge clusters and update the distance matrix based on the linkage rule (e.g. single-linkage), but this is omitted here for simplicity.

Model Evaluation

Evaluating hierarchical clustering is similar to other clustering algorithms. However, because it produces a tree of nested clusters (a dendrogram), evaluation can involve both flat clustering validation (after a cut) and hierarchy-specific metrics.

Cophenetic Correlation Coefficient (Internal)

Measures how faithfully the dendrogram preserves the pairwise distances between points.

$$\text{Cophenetic Correlation} = \text{corr}(D_{original}, D_{cophenetic})$$

$D_{original}$ is the original pairwise distances..
$D_{cophenetic}$ is the distances represented by the dendrogram.

Range: 0 to 1

Close to 1 means the clustering structure closely matches the original distances.

Silhouette Score (Internal)

Evaluates how similar each point is to its own cluster vs. others, after “cutting” the dendrogram into flat clusters. It ranges from -1 to 1:

$$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$$

$a(i)$: mean intra-cluster distance (how close point $i$ is to others in its own cluster).
$b(i)$: mean nearest-cluster distance (how close point $i$ is to points in the nearest different).

A score close to 1 means the point is well matched to its cluster.
A score near 0 means the point lies between two clusters.
A negative score indicates potential misclassification.

After segmenting customers, a high average silhouette score means most customers clearly belong to one group.

Dunn Index (Internal)

Measures the ratio between the minimum inter-cluster distance and the maximum intra-cluster distance.

$$\text{Dunn} = \frac{\min(\text{distance between clusters})}{\max(\text{cluster diameter})}$$

Higher values indicate better clustering.

Adjusted Rand Index (External)

Measures how similar the clustering is to the ground truth. Adjusts for chance grouping.

Range: -1 to 1

1: perfect match.
0: random clustering.
Negative: worse than random.

Normalized Mutual Information (External)

Measures mutual dependence between predicted clusters and ground-truth labels.

$$\text{NMI} = \frac{2 \cdot I(X; Y)}{H(X) + H(Y)}$$

$I(X; Y)$ is mutual information.
$H(X), H(Y)$ are the entropies of the clusters.

Range: 0 (no mutual info) to 1 (perfect correlation)

Alternative Algorithms

While Hierarchical Clustering is powerful for visualizing nested structures and exploring data relationships, it's not always the best choice. Several alternative clustering algorithms offer different strengths, depending on the data's shape, size, and quality. Choosing the right one depends on your specific task, data characteristics, and whether you need hard or soft cluster assignments.

DBSCAN: DBSCAN groups closely packed points and identifies outliers as noise. It is ideal for spatial data or situations with noise and irregular cluster shapes, though its performance can be sensitive to parameters like ε and minPts, and it struggles with varying densities. Learn more
k-Means: K-Means partitions data into a pre-defined number of clusters by minimizing within-cluster variance. It’s fast, scalable, and works well with well-separated, spherical clusters, but struggles with noise and non-globular shapes, and requires knowing the number of clusters in advance. Learn more
OPTICS: OPTICS extends DBSCAN to handle clusters of varying densities, making it effective for noisy datasets with heterogeneous cluster structures. It avoids a fixed epsilon value but is more complex and can be harder to interpret than DBSCAN.
Gaussian Mixture Models (GMM): GMM assumes data is generated by a mixture of Gaussian distributions, assigning probabilities to each cluster. It offers soft clustering and probabilistic interpretations, making it suitable for applications like finance or anomaly detection, but assumes Gaussian-shaped clusters and is sensitive to initialization.

Advantages and Disadvantages

Hierarchical Clustering provides an intuitive approach to exploring the structure of a dataset. Its ability to build a full tree of cluster relationships (the dendrogram) makes it especially valuable when the goal is not just to group data, but to understand how those groups relate to each other. However, its simplicity comes with trade-offs in scalability, noise sensitivity, and performance on complex datasets.

✅ Advantages:

You can choose the number of clusters later by cutting the dendrogram at a desired level.
Offers a full picture of nested data relationships, useful for exploratory data analysis and visualization.
Flexible in terms of how similarity is defined (e.g., single, complete, average, Ward).
Well-suited for detailed analysis of structured or lower-volume data.
Unlike K-Means or GMM, which can produce different results on different runs due to random initialization.

❌ Disadvantages:

Time and space complexity are $O(n^2)$ or worse; not suitable for big data without optimizations.
Early merging decisions can’t be undone, and outliers may distort the tree structure significantly.
Distance metrics become less meaningful as dimensionality increases.
Makes it harder to compare performance directly with algorithms like K-Means or GMM.
Once two points or clusters are joined, they stay grouped even if a better structure appears later.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟢 Small
Training Complexity	🔴 High

Use Case Examples

Gene Expression Analysis in Bioinformatics

Hierarchical clustering is widely used to group genes with similar expression patterns across different biological conditions. Identifying groups of genes that respond similarly to a disease or treatment and discover biologically meaningful gene families or pathways.

Customer Segmentation in Marketing

Businesses use hierarchical clustering to identify customer groups with similar purchasing behaviors or demographics. Clustering customers by their buying habits and loyalty levels.

Document and Text Grouping

Hierarchical methods are applied in Natural Language Processing to cluster documents, articles, or research papers based on topic similarity.

Image Segmentation in Computer Vision

In image processing, hierarchical clustering helps group similar pixels or regions in an image. Identifying different regions in satellite images (e.g., water, urban, vegetation).

Social Network Analysis

Used to detect communities or relationship patterns in social graphs. Finding clusters of friends or colleagues who frequently interact.

Conclusion

Hierarchical Clustering is an interpretable clustering algorithm that excels when the structure of the data is as important as the grouping itself. By building a full dendrogram, it allows analysts to explore clusters at multiple levels of granularity without the need to predefine the number of clusters.

While it’s not the best tool for all clustering problems, hierarchical clustering remains a go-to choice for interpretable, structure-focused analysis. It provides insights not just into what the clusters are, but how they’re related, making it a uniquely valuable tool in the unsupervised learning toolbox.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.