Multiple Linear Regression

Machine Learning → Supervised Learning → Regression → Linear Regression

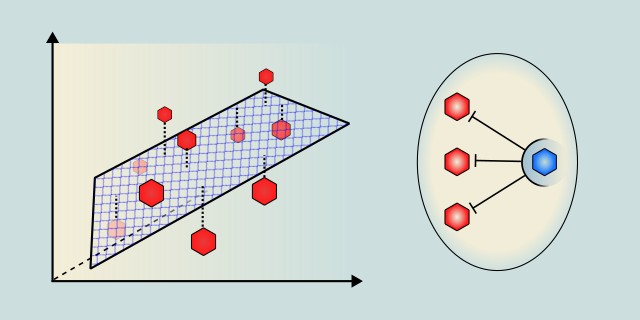
Multiple Linear Regression (MLR) is an extension of classical linear regression that allows modeling the relationship between one dependent (target) variable and multiple independent (predictor) variables. MLR is one of the most fundamental and widely used algorithms in machine learning, especially for regression tasks where the goal is to predict numerical values based on several input features. By utilizing multiple variables, the algorithm can provide better and more accurate predictions compared to simple linear regression.

To ensure that an MLR model is valid and its results are reliable, certain assumptions should be met. The most important include: linearity of the relationship between the independent and dependent variables, independence of residuals, homoscedasticity (constant variance of the errors), and normal distribution of the errors.

How It Works

Multiple Linear Regression (MLR) is a model used to predict a dependent variable $y$ based on multiple independent variables $x_1, x_2, \ldots, x_n$. The model assumes a linear relationship between the target variable and the independent variables, which can be expressed through a linear equation. While in simple linear regression we can visualize this as a line in 2D space, in MLR it becomes a plane or hyperplane in n-dimensional space, where each dimension represents one input variable.

Imagine we want to predict the monthly salary of a software developer. We know that several factors influence salary, such as years of experience, education, number of completed projects, knowledge of technologies, and geographic location.

Each of these factors can have a different level of influence on salary. Years of experience might increase salary gradually, while expertise in certain technologies could have a sharp but uneven impact. Multiple Linear Regression is able to find the best possible combination of these influences to explain (and predict) the resulting salary as accurately as possible.

Process

In practice, we can follow these steps:

We collect historical data that includes multiple input factors (e.g., years of experience, number of projects, education level) along with corresponding values of the target variable (e.g., salary amount).

Using regression analysis, we then find the equation of a multi-dimensional plane (the model) that best describes the relationship between the inputs and the output. Each input factor is assigned a coefficient that indicates how strongly that factor influences the outcome. Once we have the model (the equation), we can use it to make predictions for new cases, such as estimating the salary of a programmer with a given set of attributes that were not part of the training data.

Mathematical Foundation

The model aims to predict the target variable $y$ as a linear combination of multiple independent variables $x_1, x_2, …, x_n$. In other words, it describes the relationship between several input variables and a single output variable using a multi-dimensional equation:

$$ y = b_0 + b_1 \cdot x_1 + b_2 \cdot x_2 + … + b_n \cdot x_n + \epsilon $$

$y$ – dependent (predicted) variable
$\beta_0$ – intercept (the point where the line crosses the y-axis)
$\beta_1, \beta_2, ..., \beta_n$ – regression coefficients (weights) for each input variable
$x_1, x_2, ..., x_n$ – independent (input) variables
$\epsilon$ – random error term (the difference between actual and predicted output)

The goal is to find the coefficient values $\beta_1, \beta_2, ..., \beta_n$ that minimize the residual error between the actual and predicted values of $y$. The residual for a single observation is calculated as:

$$ \epsilon = y_i - \hat{y}_i $$

$y$ – actual value
$\hat{y}$ – value predicted by the model

To determine the optimal coefficients, we use the Ordinary Least Squares (OLS) method, which aims to minimize the sum of squared residual errors across all observations. That means we seek the coefficient values $\beta_1, \beta_2, ..., \beta_n$ that minimize the following expression:

$$ SSE = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 $$

Where $SSE$ is the Sum of Squared Errors, and $n$ is the number of observations.

For easier computation, this can be expressed in matrix form. If $X$ is the matrix of independent variables, $\beta$ is the vector of coefficients, and $y$ is the vector of target values, we can estimate the coefficients using the following formula:

$$ \hat{\beta} = (X^T X)^{-1}X^T y $$

Sample Example

Imagine you're working on a software development project and want to predict the time required to complete a task (in hours) based on the following three factors:

The developer’s experience (in years)
The task size (in lines of code)
The number of unresolved bugs

You have data from several projects, where developers took different amounts of time to complete tasks. You want to build a model that will help predict task duration based on these input variables.

Experience (years)	Task Size (lines of code)	Bugs	Time (hours)
2	1000	5	20
3	1500	3	25
5	2000	2	30
1	800	8	15

Regression formula:

$$ \text{Time} = \beta_0 + \beta_1 \cdot (\text{Experience}) + \beta_2 \cdot (\text{Task Size}) + \beta_3 \cdot (\text{Bugs}) + \epsilon $$

$\beta_0$ – intercept (base time estimate)
$\beta_1, \beta_2, \beta_3$ – coefficients that determine how much each variable affects the completion time
$\epsilon$ – random error term (the difference between actual and predicted output)

To compute the coefficients, we can express the whole problem in matrix form.

Input matrix $X$:

$$ X = \begin{bmatrix} 1 & x_{1,1} & x_{2,1} & x_{3,1} \\ 1 & x_{1,2} & x_{2,2} & x_{3,2} \\ 1 & x_{1,3} & x_{2,3} & x_{3,3} \\ \vdots & \vdots & \vdots & \vdots \\ 1 & x_{1,n} & x_{2,n} & x_{3,n} \end{bmatrix} $$

The first column of ones represents the intercept $\beta_0$
$x_1$, $x_2$, $x_3$ are the independent variable values (experience, task size, bug count) for each observation

Target vector $y$:

$$ y = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{bmatrix} $$

We compute the coefficients using the Normal Equation:

$$ \hat{\beta} = (X^T X)^{-1} X^T y $$

$X^T$ – transpose of matrix $X$
$(X^T X)^{-1}$ – inverse of $X^T X$
$X^T y$ – product of the transposed matrix and the output vector

Once we have the estimated coefficients, we can predict new values $\hat{y}$ using:

$$ \hat{y} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 $$

Use of Iterative Methods

Unlike the classical approach, iterative methods do not require processing the entire dataset at once, which makes them suitable for working with very large datasets. The most commonly used technique is gradient descent and its variants, such as stochastic gradient descent (SGD) or mini-batch gradient descent. These algorithms gradually adjust the model’s coefficients to minimize error (e.g., Mean Squared Error).

Regularization

When working with a large number of input variables, there is a risk that the model will fit the training data too well, known as overfitting. To prevent this, regularization is used by introducing a penalty term into the calculation of regression coefficients. The two most common forms are: Ridge regression (L2 regularization), which penalizes the sum of squared coefficients, and Lasso regression (L1 regularization), which penalizes the sum of the absolute values of the coefficients.

Dimensionality Reduction

With a very high number of input variables, not only does the computational complexity increase, but also the risk that not all variables are informative or independent. A solution to this problem is dimensionality reduction, which reduces the number of variables without significant loss of information. One of the most well-known techniques is Principal Component Analysis (PCA), which transforms the original variables into a new set of so-called principal components. These components capture as much variability in the data as possible while eliminating redundancy and multicollinearity among the variables.

👉 A detailed explanation of this method can be found in the section: Principal Component Analysis

Code Example

The following example uses the normal equation to compute the coefficients for Multiple Linear Regression. First, we construct the input matrix (X) including the intercept term, and the target vector (y). Using matrix transposition, multiplication, and inversion, we calculate the optimal values of the coefficients $\beta$. These coefficients are then used to predict the output for a new set of input values. The entire process demonstrates how to build a predictive model in the form of a linear equation based on historical data.

use nalgebra::{DMatrix, DVector};

/// Computes regression coefficients using the Normal Equation:
/// β = (Xᵀ X)^(-1) Xᵀ y
fn normal_equation(x: &DMatrix<f64>, y: &DVector<f64>) -> DVector<f64> {
    let x_t = x.transpose();
    let x_t_x = &x_t * x;
    let x_t_x_inv = x_t_x
        .try_inverse()
        .expect("Matrix XᵀX is not invertible");
    let x_t_y = &x_t * y;

    x_t_x_inv * x_t_y
}

fn main() {    
    // Design matrix with intercept term (first column = 1s)
    // Each row represents a data point with features x₁, x₂, ..., and an intercept term
    let x = DMatrix::from_row_slice(3, 3, &[
        1.0, 1.0, 2.0,  // row 1
        1.0, 2.0, 1.0,  // row 2
        1.0, 3.0, 3.0,  // row 3
    ]);

    // Target values
    // Corresponding y values for the design matrix
    // y = [6, 8, 14]
    let y = DVector::from_row_slice(&[6.0, 8.0, 14.0]);

    // Compute coefficients
    let beta = normal_equation(&x, &y);

    println!("Regression coefficients (β):\n{}", beta);

    // Predict y for x₁ = 4, x₂ = 2 (include intercept 1.0)
    let input = DVector::from_row_slice(&[1.0, 4.0, 2.0]);
    let prediction = beta.dot(&input);

    println!("Prediction for x₁ = 4, x₂ = 2: {}", prediction);
}

Model Evaluation – Prediction Error

It is always important to verify how accurate our model is. This helps determine whether linear regression is even appropriate. If the error is large, the relationship might be nonlinear, or the data may be too scattered. It can also help identify problematic data points or outliers.

To evaluate the model, we use various error metrics that quantify the difference between the actual values and the model’s predictions:

Residual

A residual tells us how much a specific prediction deviated from the actual result.

It is the difference between the true value and the predicted value:

$$ \varepsilon_i = y_i - \hat{y}_i $$

👉 A detailed explanation of residual can be found in the section: Residual

MSE (Mean Squared Error)

MSE penalizes larger errors more than smaller ones (because the error is squared).

It represents the average squared difference between the actual and predicted values:

$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$

👉 A detailed explanation of MSE can be found in the section: Mean Squared Error

RMSE (Root Mean Squared Error)

RMSE has the same units as the original values, making it more intuitive to interpret.

It represents the average squared difference between the actual and predicted values:

$$ \text{RMSE} = \sqrt{\text{MSE}} $$

👉 A detailed explanation of RMSE can be found in the section: Root Mean Squared Error

R² (Coefficient of Determination)

R² indicates how much of the variability in the data can be explained by the model:

$$ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} $$

Close to 1 – the model explains the variability in the data very well.
Close to 0 – the model explains very little of the variability.

👉 A detailed explanation of R² can be found in the section: R² Coefficient of Determination

Alternative Algorithms

Multiple Linear Regression is an effective tool for modeling relationships between multiple variables, but in practice, there are situations where alternative approaches may be more suitable. For example, if the relationship between variables is non-linear, or if the dataset is very large and complex, models such as decision trees, random forests, or neural networks may offer better accuracy and flexibility. Additionally, when input variables are highly correlated, regularization techniques like Ridge or Lasso regression can help reduce multicollinearity and improve the model’s generalization.

Ridge and Lasso Regression: Extensions of linear regression with regularization, which help prevent model overfitting.
Polynomial Regression: Allows modeling of non-linear relationships by applying linear regression to expanded feature sets.
Decision Tree Regression: Tree-based models capable of handling complex, non-linear relationships and interactions; less sensitive to noise and outliers.Learn more
Support Vector Regression: A good choice when working with small datasets and non-linear relationships. Learn more

Advantages and Disadvantages

✅ Advantages:

Interpretable results and coefficients.
Allows evaluation of the significance of individual variables.
Simple and fast to implement.
Can be extended with regularization (Ridge, Lasso).
Suitable for medium-sized datasets.

❌ Disadvantages:

Assumes a linear relationship between variables
Sensitive to multicollinearity (strong correlation between inputs).
Prone to outliers.
Assumes independent and homoskedastic errors.
Limited in modeling non-linear relationships.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟡 Medium / 🔴 Large
Training Complexity	🟡 Medium

Use Case Examples

Real Estate Price Estimation

Predicting real estate prices based on various factors such as area size, number of rooms, distance from city center, building age, or access to public transportation.

Marketing ROI Analysis

Evaluating the impact of different marketing channels (e.g., social media, television, online ads) on product sales.

Medical Risk Prediction

Estimating the risk of heart disease or diabetes based on a combination of variables such as age, BMI, cholesterol level, and blood pressure.

Academic Performance Forecast

Predicting a student's final score based on factors like study hours, lecture attendance, previous grades, and sleep quality.

Energy Consumption Modeling

Modeling energy consumption in households or businesses based on outdoor temperature, number of people, appliances, and heating method.

Conclusion

Multiple Linear Regression is an effective method that allows us to model the relationship between multiple input variables and a single target variable. It is suitable for tasks where a linear dependency exists and where we not only want to predict outcomes but also understand how individual factors influence the result. Thanks to its interpretability, MLR is often the first choice in data analysis. It can be used whenever we have several quantitative inputs, want insight into their influence on the outcome, and assume the relationship is approximately linear.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.