Decision Tree Classification

Machine Learning → Supervised Learning → Classification → Single Label Classification → Binary Classification

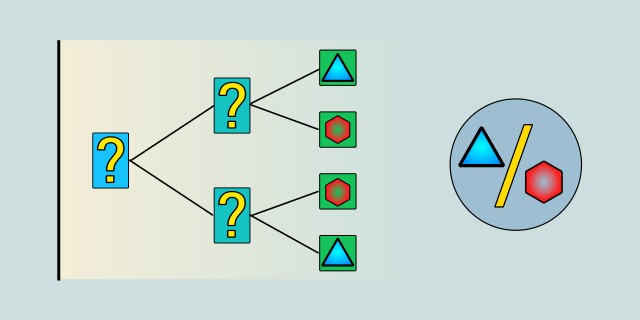
The Decision Tree algorithm is supervised learning method for classification and regression tasks. In classification, it works by learning simple decision rules inferred from the features of the input data. Its structure resembles a flowchart, where each internal node represents a decision based on a feature, each branch represents the outcome of that decision, and each leaf node represents a final class label.

Decision trees are intuitive, easy to interpret, and capable of capturing complex patterns in data without requiring advanced preprocessing. Because of their transparent structure, they are often favored in applications where explainability is important, such as finance, healthcare, and policy making.

In a classification context, the algorithm splits the dataset into subsets based on feature values, recursively building branches until it reaches a point where further splitting no longer improves prediction. Each path from the root to a leaf represents a classification rule, making the model interpretable and easy to visualize.

How It Works

A decision tree for classification works by asking a series of simple yes-or-no questions about the input data. These questions are based on the values of the features in the dataset. The goal is to gradually divide the data into smaller and more specific groups until each group contains mostly (or only) examples from a single class.

Let's imagine that we are trying to classify whether a fruit is an apple, an orange, or a banana. The decision tree could work as follows:

1. question: Is the fruit red?

If yes, it might be an apple.
If no, move to the next question.

2. question: Is the shape long and curved?

If yes, it's likely a banana.
If no, it might be an orange.

Each question forms a node in the tree, and each answer leads to another question or to a final decision (called a leaf node). The tree keeps splitting the data like this, creating branches, until each path leads to a classification. The algorithm decides which question to ask at each step by looking for the feature that best separates the data. For example, if one feature (like "color") cleanly separates apples from the others, it will be used near the top of the tree. This process continues recursively: the data is split, then the algorithm repeats the process on each split.

The tree grows by repeatedly splitting the data into smaller subsets, continuing this process until one of several stopping conditions is met: all examples in a branch belong to the same class, a predefined maximum depth is reached, or further splitting no longer provides a meaningful improvement in classification accuracy. This step-by-step decision-making process makes the model highly interpretable. We can clearly see how the prediction is made by following the path from the root of the tree to the leaf node, with each split representing a simple, understandable rule.

Mathematical Foundation

The core principle behind decision trees is to divide the dataset in a way that results in subsets that are as homogeneous as possible with respect to the target class. In other words, the algorithm tries to group the data so that each resulting branch contains instances that belong mostly, or entirely to a single class. To evaluate the quality of each split, decision trees rely on impurity measures that quantify how mixed or pure a node is at any point in the tree-building process.

Gini Impurity

Gini impurity measures how often a randomly chosen element from a set would be incorrectly labeled if it were randomly labeled according to the class distribution in that subset.

$$Gini(t) = 1 - \sum_{i=1}^{C} p_i^2$$

$p_i$ is the proportion of examples of class $i$ at node $t$.
$C$ is the total number of classes.

Gini impurity of 0 means the node is pure (all examples belong to the same class).

Entropy (Information Gain)

Entropy measures the amount of uncertainty or disorder in the dataset. Lower entropy means higher purity.

$$Entropy(t) = - \sum_{i=1}^{C} p_i \log_2 p_i$$

Like Gini, $p_i$ is the proportion of examples of class $i$ at node $t$. Entropy is 0 when the node contains only one class.

Information Gain

To choose the best feature to split on at each step, the algorithm calculates the information gain, which is the reduction in impurity after a split.

For entropy:

$$Information\ Gain = Entropy(parent) - \sum_{k=1}^{K} \frac{N_k}{N} \cdot Entropy(k)$$

$N_k$ is the number of samples in child node $k$.
$N$ is the total number of samples in the parent node.
$K$ is the number of child nodes (usually 2 for binary splits).

The algorithm selects the feature and threshold that maximize information gain, resulting in the most "pure" child nodes.

Stopping Criteria

The tree stops splitting when when one of the following conditions is met:

All examples in a node belong to the same class, meaning the node is already perfectly pure.
A predefined maximum depth has been reached, limiting how many levels the tree can grow.
The number of samples in the node is below a minimum threshold, so further splitting would be unreliable or not statistically meaningful.
The improvement in impurity (such as Gini or entropy) from a potential split is smaller than a defined minimum gain, suggesting the split does not add real value.

Code Example

The DecisionTree struct represents a node in the decision tree, which can either be an internal decision node or a leaf node with a predicted label.

Gini Impurity

The gini_impurity function calculates the Gini Impurity of a set of labels. Gini Impurity measures how often a randomly chosen element from the set would be incorrectly labeled if it were randomly labeled according to the distribution of labels in the subset. The goal of the algorithm is to minimize impurity by choosing the best feature and threshold to split on. A lower Gini value indicates a better (purer) split.

Best Split

The best_split function searches for the optimal feature and threshold to split the dataset. It evaluates all possible splits by calculating the Gini Impurity for each, ultimately selecting the one that minimizes the weighted impurity of the child nodes.

Training

The train function recursively builds the decision tree. At each node, it selects the feature and threshold that yields the best split (i.e., lowest Gini Impurity). This process continues until a stopping condition is met, typically when all labels in a node are the same, at which point the node becomes a leaf. The label assigned to the leaf corresponds to the majority class of samples in that node.

Prediction

The predict function classifies a given input sample by traversing the tree from the root. At each decision node, it compares the relevant feature of the sample to the node’s threshold and follows the left or right branch accordingly. Once a leaf node is reached, its label is returned as the prediction.

Dependencies

Add to your Cargo.toml:

[dependencies]
ndarray = "0.15.4"

Code

use ndarray::Array2;
use std::cmp::Ordering;
use std::collections::HashMap;

#[derive(Debug, Clone)]
struct DecisionTree {
    feature: Option<usize>,
    threshold: Option<f64>,
    left: Option<Box<DecisionTree>>,
    right: Option<Box<DecisionTree>>,
    label: Option<String>,
}

impl DecisionTree {
    // Function to calculate Gini Impurity of a dataset
    fn gini_impurity(labels: &Vec<String>) -> f64 {
        let mut label_counts = HashMap::new();
        let total = labels.len() as f64;

        for label in labels {
            *label_counts.entry(label).or_insert(0) += 1;
        }

        label_counts
            .values()
            .map(|&count| {
                let p = count as f64 / total;
                p * (1.0 - p)
            })
            .sum()
    }

    // Function to split the dataset based on a feature and threshold
    fn split_dataset(data: &Array2<f64>, labels: &Vec<String>, feature: usize, threshold: f64) -> (Vec<String>, Vec<String>, Array2<f64>, Array2<f64>) {
        let mut left_data = Vec::new();
        let mut right_data = Vec::new();
        let mut left_labels = Vec::new();
        let mut right_labels = Vec::new();

        for i in 0..data.nrows() {
            if data[[i, feature]] <= threshold {
                left_data.push(data.row(i).to_owned());
                left_labels.push(labels[i].clone());
            } else {
                right_data.push(data.row(i).to_owned());
                right_labels.push(labels[i].clone());
            }
        }

        let left_data = if !left_data.is_empty() {
            Array2::from_shape_vec((left_data.len(), left_data[0].len()), left_data.into_iter().flatten().collect()).unwrap()
        } else {
            Array2::from_shape_vec((0, data.ncols()), vec![]).unwrap()
        };
        let right_data = if !right_data.is_empty() {
            Array2::from_shape_vec((right_data.len(), right_data[0].len()), right_data.into_iter().flatten().collect()).unwrap()
        } else {
            Array2::from_shape_vec((0, data.ncols()), vec![]).unwrap()
        };

        (left_labels, right_labels, left_data, right_data)
    }

    // Function to find the best split for the data
    fn best_split(data: &Array2<f64>, labels: &Vec<String>) -> (usize, f64) {
        let mut best_gini = f64::MAX;
        let mut best_feature = 0;
        let mut best_threshold = 0.0;

        for feature in 0..data.ncols() {
            let mut thresholds: Vec<f64> = data.column(feature).to_owned().into_iter().collect();
            thresholds.sort_by(|a, b| a.partial_cmp(b).unwrap_or(Ordering::Equal));

            for &threshold in &thresholds {
                let (left_labels, right_labels, _, _) = DecisionTree::split_dataset(data, labels, feature, threshold);
                let gini_left = DecisionTree::gini_impurity(&left_labels);
                let gini_right = DecisionTree::gini_impurity(&right_labels);
                let gini = gini_left * (left_labels.len() as f64 / labels.len() as f64)
                          + gini_right * (right_labels.len() as f64 / labels.len() as f64);

                if gini < best_gini {
                    best_gini = gini;
                    best_feature = feature;
                    best_threshold = threshold;
                }
            }
        }

        (best_feature, best_threshold)
    }

    // Function to train the decision tree recursively
    fn train(data: &Array2<f64>, labels: &Vec<String>, depth: usize) -> DecisionTree {
        // If all labels are the same, return a leaf node
        if labels.iter().all(|label| label == &labels[0]) {
            return DecisionTree {
                feature: None,
                threshold: None,
                left: None,
                right: None,
                label: Some(labels[0].clone()),
            };
        }

        // Find the best feature and threshold for splitting
        let (best_feature, best_threshold) = DecisionTree::best_split(data, labels);

        // Split the dataset
        let (left_labels, right_labels, left_data, right_data) =
            DecisionTree::split_dataset(data, labels, best_feature, best_threshold);

        // If either split is empty, return a leaf node with the most common label
        if left_labels.is_empty() || right_labels.is_empty() {
            let mut label_counts = HashMap::new();
            for label in labels {
                *label_counts.entry(label).or_insert(0) += 1;
            }
            let majority_label = label_counts.into_iter().max_by_key(|&(_, count)| count).unwrap().0.clone();
            return DecisionTree {
                feature: None,
                threshold: None,
                left: None,
                right: None,
                label: Some(majority_label),
            };
        }

        // Recursively build the left and right subtrees
        let left_tree = DecisionTree::train(&left_data, &left_labels, depth + 1);
        let right_tree = DecisionTree::train(&right_data, &right_labels, depth + 1);

        DecisionTree {
            feature: Some(best_feature),
            threshold: Some(best_threshold),
            left: Some(Box::new(left_tree)),
            right: Some(Box::new(right_tree)),
            label: None,
        }
    }

    // Function to make a prediction
    fn predict(&self, sample: &Array2<f64>) -> String {
        if let Some(ref label) = self.label {
            return label.clone();
        }

        let feature = self.feature.unwrap();
        let threshold = self.threshold.unwrap();

        if sample[[0, feature]] <= threshold {
            self.left.as_ref().unwrap().predict(sample)
        } else {
            self.right.as_ref().unwrap().predict(sample)
        }
    }
}

fn main() {
    // Example dataset (features: height, weight; label: A or B)
    let data = Array2::from_shape_vec(
        (6, 2),
        vec![
            1.0, 2.0,
            1.5, 2.5,
            3.0, 3.5,
            3.5, 4.0,
            5.0, 5.5,
            5.5, 6.0,
        ],
    )
    .unwrap();

    let labels = vec![
        "A".to_string(),
        "A".to_string(),
        "B".to_string(),
        "B".to_string(),
        "B".to_string(),
        "B".to_string(),
    ];

    // Train the decision tree classifier
    let tree = DecisionTree::train(&data, &labels, 0);

    // Example query point
    let query_point = Array2::from_shape_vec((1, 2), vec![4.0, 4.5]).unwrap();
    
    // Predict the label for the query point
    let prediction = tree.predict(&query_point);
    println!("Predicted label: {}", prediction);
}

Output

Predicted label: B

This means that the decision tree predicted the label "B" for the query point [4.0, 4.5].

Model Evaluation

In the case of k-Nearest Neighbors (k-NN) for classification, several standard metrics are used to assess model quality. Each provides insight into different aspects of the model's behavior.

Accuracy

Accuracy is the most basic metric that shows the proportion of correct predictions out of the total number of predictions. It indicates what fraction of all predictions the model identified correctly.

$$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total number of predictions}}$$

If the dataset is imbalanced (e.g., 95% of class 0), accuracy can be misleading.

Accuracy of 90% or higher is generally considered good for balanced and noise-free datasets.

👉 A detailed explanation of Accuracy can be found in the section: Accuracy

Precision

Precision tells us how many of the predicted positive results were actually correct. It is important when avoiding false positives is critical (for example, in medicine where a wrong diagnosis can have serious consequences).

$$\text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}}$$

Important when false positives are problematic (e.g., labeling a valid email as spam, or medicine diagnostics).

👉 A detailed explanation of Precision can be found in the section: Precision

Recall (Sensitivity)

Recall tells us how many of the actual positive cases the model correctly identified. It is important when minimizing false negatives is necessary, i.e., situations where the model misses real positive cases (for example, in cancer detection, where failing to detect a positive case can be dangerous).

$$\text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}}$$

Crucial when we want to avoid missing any positive cases (e.g., disease detection).

👉 A detailed explanation of Recall can be found in the section: Recall

F1 Score

The F1 score is the harmonic mean of precision and recall. It is very useful when both precision and recall need to be balanced. This metric is valuable when we want to consider both the correctness of positive predictions and the ability to find all actual positive cases.

$$\text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$$

Especially useful for imbalanced class distributions.

F1 score of 0.8 or higher is generally considered good.

👉 A detailed explanation of F1 Score can be found in the section: F1 Score

Confusion Matrix

A confusion matrix is a table that summarizes the performance of a classification model by showing the counts of true positives, false positives, true negatives, and false negatives. It provides a detailed breakdown of how the model’s predictions compare to the actual labels and helps identify specific types of errors.

	Predicted Positive	Predicted Negative
Actual Positive	TP	FN
Actual Negative	FP	TN

TP (True Positives) – Correctly predicted positive cases.
TN (True Negatives) – Correctly predicted negative cases.
FP (False Positives) – Incorrectly predicted positive cases.
FN (False Negatives) – Incorrectly predicted negative cases.

Cross-Validation Accuracy

Cross-validation accuracy measures how well a model performs on unseen data by repeatedly splitting the dataset into training and testing parts. For example, in k-fold cross-validation, the data is divided into k parts, and the model is trained k times, each time leaving out a different part for testing. This helps obtain a more reliable estimate of model performance than a single train-test split.

Low variability in performance across cross-validation folds suggests that the model is stable and generalizes well.

Alternative Algorithms

While Decision Trees are useful, several other algorithms are commonly used for classification problems. Each has its own strengths and ideal use cases.

Random Forest: An ensemble method that builds multiple decision trees and aggregates their predictions, usually by majority vote. It tends to be more accurate and robust than a single tree and reduces overfitting, but it is less interpretable and more computationally intensive. Learn more
Support Vector Machines (SVM): SVM finds the hyperplane that best separates classes by maximizing the margin between them. It performs well in high-dimensional spaces with clear margins, but it is less intuitive, sensitive to parameter choices, and slower on large datasets. Learn more
k-Nearest Neighbors (k-NN): This algorithm classifies new samples based on the majority label among the k closest points in the training set. It is easy to understand and requires no training phase, but can be slow at prediction time and is sensitive to irrelevant features and feature scaling. Learn more
Logistic Regression: A linear model that estimates the probability of class membership using input features. It is simple to implement and works well when data is linearly separable, but struggles with complex, non-linear relationships. Learn more
Gradient Boosting Machines (GBM): GBM builds decision trees sequentially, with each tree correcting the errors of the previous ones. It can achieve high accuracy and is highly flexible, but often requires careful tuning, is harder to interpret, and can be computationally expensive.

Advantages and Disadvantages

Decision Trees offer several practical benefits that make them a popular choice for classification tasks, especially when interpretability is important. However, they also have limitations that can impact performance, particularly on complex or imbalanced datasets.

✅ Advantages:

Mimic human decision-making processes, making their results transparent and easy to explain without requiring deep technical knowledge.
Decision trees can naturally manage a mix of feature types without needing extensive preprocessing.
They do not assume any specific data distribution and can capture complex, non-linear relationships.
No need for feature scaling or normalization, which simplifies the data pipeline.
Decision trees can naturally extend beyond binary classification to multiple classes.

❌ Disadvantages:

Without constraints, trees can become overly complex and fit noise in the training data, harming generalization.
Minor changes in the data can lead to significantly different trees, affecting stability.
Features with many unique values can dominate splits, even if they are less informative.
Single decision trees often underperform compared to more advanced techniques like random forests or gradient boosting.
Trees might favor the majority class if class distribution is skewed, requiring special handling or metric adjustments.

Quick Recommendations

Criterion	Recommendation
Dataset Size	🟢 Small / 🟡 Medium / 🔴 Large
Training Complexity	🟢 Low

Use Case Examples

Medical Diagnosis

Predicting diseases based on patient symptoms and test results, helping doctors make informed decisions.

Customer Churn Prediction

Identifying customers likely to stop using a service by analyzing their behavior and engagement patterns.

Credit Risk Assessment

Evaluating loan applicants to decide whether they pose a high risk of default based on financial history and demographics.

Fraud Detection

Detecting fraudulent transactions by spotting unusual patterns in financial data.

Marketing Campaign Targeting

Segmenting customers to tailor marketing efforts and improve conversion rates by predicting response likelihood.

Conclusion

Decision trees provide an intuitive method for classification tasks. Their ability to work with both numerical and categorical data, along with their clear interpretability, makes them a valuable tool when transparency in decision-making is essential. However, they can be prone to overfitting and may have difficulty handling noisy or imbalanced datasets. For these reasons, it is often helpful to explore ensemble methods or alternative algorithms when the highest accuracy is required. Overall, decision trees serve as an excellent starting point for classification problems by offering a good balance between simplicity and effectiveness.

External resources:

Example code in Rust available on 👉 GitHub Repository

Feedback

Found this helpful? Let me know what you think or suggest improvements 👉 Contact me.