Linear Regression
Linear regression is a fundamental algorithm used for predicting a continuous target variable based on one or more input features. It assumes a linear relationship between the input features and the target variable.
What is the complexity of the relationship you're trying to model?
Do you need to predict based on one feature or multiple features?
Tips:
- If your prediction depends on just a single input variable, go with Simple Linear Regression.
- If your prediction depends on multiple features (e.g., size, age, location), choose Multiple Linear Regression.
Simple Linear Regression
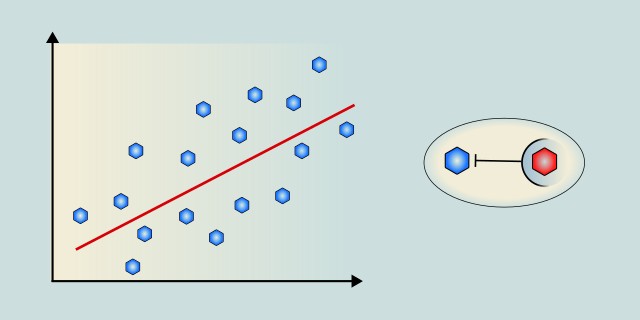
Simple Linear Regression is a basic statistical method that models the relationship between a single independent variable and a continuous dependent variable by fitting a straight line. It assumes a linear relationship and predicts outcomes based on this line.
This method is easy to interpret and implement, making it a good starting point for regression problems. It is limited to modeling linear relationships and cannot capture complexities like interactions or non-linear patterns. It’s sensitive to outliers and assumes homoscedasticity (constant variance) and normally distributed errors. Simple Linear Regression is mostly used when you have one predictor variable and want to understand or predict a target.
Use Case Examples:
- House Price Prediction: Estimating house prices based on size or location.
- Salary Estimation: Predicting salary based on years of experience.
- Advertising Impact: Analyzing sales changes relative to advertising spend.
- Exam Score Prediction: Forecasting exam results based on hours studied.
- GDP Growth Forecast: Predicting GDP growth from historical economic indicators.
| Criterion | Recommendation |
|---|---|
| Dataset Size | 🟢 Small / 🟡 Medium |
| Training Complexity | 🟢 Low |
Multiple Linear Regression
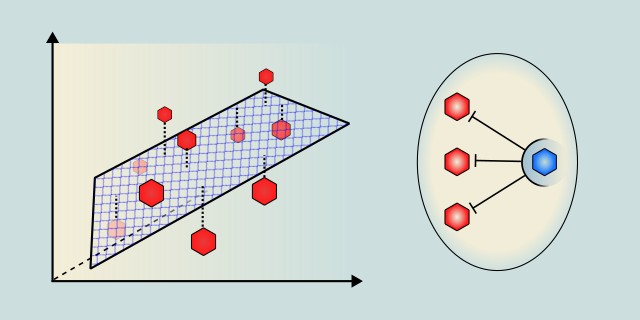
Multiple Linear Regression extends simple linear regression by modeling the relationship between two or more independent variables and a continuous dependent variable. It fits a linear equation to observed data with multiple predictors.
This method helps analyze the impact of several factors simultaneously on a target variable. It assumes a linear relationship between predictors and the outcome, and is sensitive to multicollinearity (correlation between predictors). Like simple linear regression, it assumes normally distributed residuals and constant variance. It is widely used when multiple features influence the result and interpretability remains important.
Use Case Examples:
- House Price Prediction: Predicting prices using features like size, location, and number of rooms.
- Employee Salary Estimation: Estimating salary based on experience, education, and job role.
- Sales Forecasting: Modeling sales influenced by advertising, seasonality, and competitor prices.
- Health Outcome Prediction: Predicting patient recovery time from age, treatment type, and medical history.
- Energy Consumption: Estimating energy use based on weather, appliance usage, and occupancy.
| Criterion | Recommendation |
|---|---|
| Dataset Size | 🟡 Medium / 🔴 Large |
| Training Complexity | 🟡 Medium |